题目内容
12、如果△ABC中，∠A，∠B，∠C的相邻的外角之比为4：2：3，则∠BAC的度数为（ ）
分析：因为三角形的外角和为360°，可首先求出与∠A，∠B，∠C相邻的三个外角的度数，则可求出∠BAC的度数．
解答：解：∵∠A，∠B，∠C的相邻的外角之比为4：2：3，
可设∠A，∠B，∠C分别为：4x，2x，3x．；
则有4x+2x+3x=360°，
解得：x=40°，则4x=160°，
∴∠BAC=180°-160°=20°．
故选A．
可设∠A，∠B，∠C分别为：4x，2x，3x．；
则有4x+2x+3x=360°，
解得：x=40°，则4x=160°，
∴∠BAC=180°-160°=20°．
故选A．
点评：本题主要考查三角形的外角性质及三角形的内角和定理，解题的关键是熟练掌握三角形的外角性质定理，即三角形的一个外角等于与它不相邻的两个内角之和．
练习册系列答案
相关题目
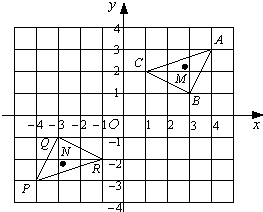15、如图，△PQR是△ABC经过某种变换后得到的图形．如果△ABC中任意一点M的坐标为（a，b），那么它的对应点N的坐标为如果△ABC中，∠A：∠B：∠C=1：2：3，那么BC：AC：AB的值是（ ）
| A、1：2：3 | ||
| B、3：2：1 | ||
C、1：
| ||
D、1：2：
|
