题目内容
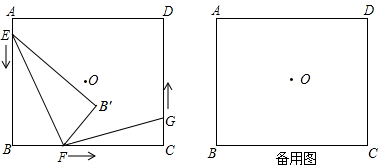
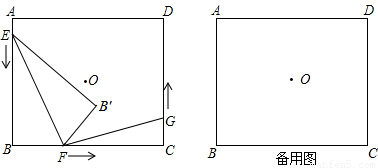
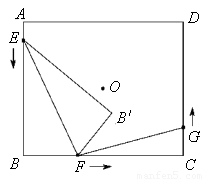
 如图,点E为矩形ABCD的边AD上一点,BE=BC,EF平分∠AEB交AB于点F,连FC.
如图,点E为矩形ABCD的边AD上一点,BE=BC,EF平分∠AEB交AB于点F,连FC.(1)求证:EF⊥EC;
(2)
| AB |
| BC |
| EC |
| FC |
分析:(1)由四边形ABCD是矩形与BC=BE,易证得∠CED=∠CEB=
∠DEB,又由∠AEF=∠BEF=
∠AEB,即可证得EF⊥EC;
(2)易证得点B,C,E,F四点共圆,∠BEF=∠BCF,又由等角的余角相等,证得∠BCF=∠ECD,由∠FBC=∠D=90°,可证得△FBC∽△EDC,继而证得
=
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)易证得点B,C,E,F四点共圆,∠BEF=∠BCF,又由等角的余角相等,证得∠BCF=∠ECD,由∠FBC=∠D=90°,可证得△FBC∽△EDC,继而证得
| AB |
| BC |
| EC |
| FC |
解答: 证明:(1)∵四边形ABCD是矩形,
证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CED=∠ECB,
∵BC=BE,
∴∠ECB=∠CEB,
∴∠CED=∠CEB=
∠DEB,
∵EF平分∠AEB,
∴∠AEF=∠BEF=
∠AEB,
∴∠FEC=∠FEB+∠CEB=
∠AEB+
∠DEB=
(∠AEB+∠DEB)=
×180°=90°,
∴EF⊥EC;
(2)∵EF⊥BC,
∴∠FEC=90°,
∵∠FBC=90°,
∴∠FBC+∠FEC=180°,
∴点B,C,E,F四点共圆,
∴∠BEF=∠BCF,
∵∠BEF+∠DEC=90°,∠ECD+∠DEC=90°,
∴∠BCF=∠ECD,
∵∠FBC=∠D=90°,
∴△FBC∽△EDC,
∴
=
,
∵CD=AB,
∴
=
.
 证明:(1)∵四边形ABCD是矩形,
证明:(1)∵四边形ABCD是矩形,∴AD∥BC,
∴∠CED=∠ECB,
∵BC=BE,
∴∠ECB=∠CEB,
∴∠CED=∠CEB=
| 1 |
| 2 |
∵EF平分∠AEB,
∴∠AEF=∠BEF=
| 1 |
| 2 |
∴∠FEC=∠FEB+∠CEB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EF⊥EC;
(2)∵EF⊥BC,
∴∠FEC=90°,
∵∠FBC=90°,
∴∠FBC+∠FEC=180°,
∴点B,C,E,F四点共圆,
∴∠BEF=∠BCF,
∵∠BEF+∠DEC=90°,∠ECD+∠DEC=90°,
∴∠BCF=∠ECD,
∵∠FBC=∠D=90°,
∴△FBC∽△EDC,
∴
| FC |
| EC |
| BC |
| CD |
∵CD=AB,
∴
| AB |
| BC |
| EC |
| FC |
点评:此题考查了相似三角形的判定与性质、矩形的性质、垂直的定义以及等腰三角形的性质.此题难度较大,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
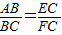 .
.