题目内容
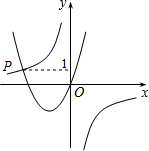如图，已知函数y=-| 3 |
| x |
| 3 |
| x |
分析：先根据点P的纵坐标为1求出x的值，再把于x的方程ax2+bx+
=0化为于x的方程ax2+bx=-
的形式，此方程就化为求
函数y=-
与y=ax2+bx（a＞0，b＞0）的图象交点的横坐标，由求出的P点坐标即可得出结论．
| 3 |
| x |
| 3 |
| x |
函数y=-
| 3 |
| x |
解答：解：∵P的纵坐标为1，
∴1=-
，
∴x=-3，
∵ax2+bx+
=0化为于x的方程ax2+bx=-
的形式，
∴此方程的解即为两函数图象交点的横坐标的值，
∴x=-3．
故答案为：x=-3．
∴1=-
| 3 |
| x |
∴x=-3，
∵ax2+bx+
| 3 |
| x |
| 3 |
| x |
∴此方程的解即为两函数图象交点的横坐标的值，
∴x=-3．
故答案为：x=-3．
点评：本题考查的是二次函数的图象与反比例函数图象的交点问题，能把方程的解化为两函数图象的交点问题是解答此题的关键．
练习册系列答案
相关题目
如图，已知函数y1=kx+b与函数y2=| m |
| x |
| m |
| x |
| A、x1=1，x2=-3 |
| B、x1=-1，x2=3 |
| C、x1=1，x2=-1 |
| D、x1=3，x2=-3 |
14、如图，已知函数y=3x+b和y=ax-3的图象交于点P（-2，-5），则根据图象可得不等式3x+b＞ax-3的解集在数轴上表示正确的是（ ）
12、如图，已知函数y=x+b和y=ax+3的图象交点为P，则不等式x+b＞ax+3的解集为
如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于
如图，已知函数