题目内容
在四边形ABCD中,已知△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则边CD的长为________.
4
分析:首先根据题意作出图形,然后以CD为边作等边△CDE,连接AE.易证得△BCD≌△ACE,则可得AE=BD=5,又由∠ADC=30°,可求得∠ADE=90°,然后由股定理可求得DE的长,继而可求得边CD的长.
解答: 解:如图,以CD为边作等边△CDE,连接AE.
解:如图,以CD为边作等边△CDE,连接AE.
∴CD=CE=DE,∠DCE=∠CDE=60°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵∠BCD=∠BCA+∠ACD,∠ACE=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
∵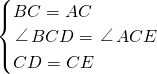 ,
,
∴△BCD≌△ACE(SAS),
∴AE=BD=5.
又∵∠ADC=30°,
∴∠ADE=∠ADC+∠CDE=90°.
在Rt△ADE中,AE=5,AD=3,
∴DE= =4,
=4,
∴CD=DE=4.
故答案为:4.
点评:此题考查了等边三角形的性质、全等三角形的判定与性质以及勾股定理等知识.此题难度较大,解题的关键是准确作出辅助线,注意数形结合思想的应用.
分析:首先根据题意作出图形,然后以CD为边作等边△CDE,连接AE.易证得△BCD≌△ACE,则可得AE=BD=5,又由∠ADC=30°,可求得∠ADE=90°,然后由股定理可求得DE的长,继而可求得边CD的长.
解答:
 解:如图,以CD为边作等边△CDE,连接AE.
解:如图,以CD为边作等边△CDE,连接AE.∴CD=CE=DE,∠DCE=∠CDE=60°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵∠BCD=∠BCA+∠ACD,∠ACE=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
∵
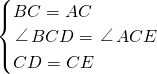 ,
,∴△BCD≌△ACE(SAS),
∴AE=BD=5.
又∵∠ADC=30°,
∴∠ADE=∠ADC+∠CDE=90°.
在Rt△ADE中,AE=5,AD=3,
∴DE=
 =4,
=4,∴CD=DE=4.
故答案为:4.
点评:此题考查了等边三角形的性质、全等三角形的判定与性质以及勾股定理等知识.此题难度较大,解题的关键是准确作出辅助线,注意数形结合思想的应用.

练习册系列答案
相关题目
 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?