题目内容
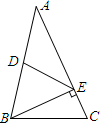
20．
如图，△BDE∽△BCA，若$\frac{BD}{BC}$=$\frac{2}{3}$，DE=6，则AC的长度是9．
分析 由相似三角形的性质得出对应边成比例，即可得出AC的长度．
解答 解：∵△BDE∽△BCA，
∴$\frac{DE}{AC}$=$\frac{BD}{BC}$=$\frac{2}{3}$，
即$\frac{6}{AC}=\frac{2}{3}$，
解得：AC=9；
故答案为：9．
点评 本题考查了相似三角形的性质；熟练掌握相似三角形的性质，由相似三角形的性质得出应边成比例是解决问题的关键．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
10．下列结论正确的个数有（ ）
①有两边和一角对应相等的两个三角形全等；
②三角形三边的垂直平分线相交于一点；
③有两边对应相等的两个直角三角形全等；
④直线不是轴对称图形．
①有两边和一角对应相等的两个三角形全等；
②三角形三边的垂直平分线相交于一点；
③有两边对应相等的两个直角三角形全等；
④直线不是轴对称图形．
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
11．下列计算正确的是（ ）
| A． | $\frac{x^6}{x^3}={x^2}$ | B． | $\frac{x+y}{x+y}=0$ | C． | $\frac{y+a}{x+a}=\frac{y}{x}$ | D． | $\frac{-x+y}{x-y}$=-1 |
8．
小明不慎把家里的圆形镜子打碎了，其中四块碎片如图所示，为了配到与原来大小一样的圆形镜子，小明带到商店去的一块碎片应该是（ ）
小明不慎把家里的圆形镜子打碎了，其中四块碎片如图所示，为了配到与原来大小一样的圆形镜子，小明带到商店去的一块碎片应该是（ ）| A． | 第一块 | B． | 第二块 | C． | 第三块 | D． | 第四块 |
如图，△ABC中，E在AC上，且BE⊥AC．D为AB中点，若DE=5，AE=8，则BE的长为6．
如图，一个矩形广场的长为60m，宽为40m，广场内两条纵向小路的宽均为2m，如果设两条横向小路的宽都为xm，那么当x为多少时，小路内外边缘所围成的两个矩形相似．