题目内容
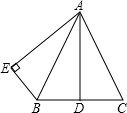 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.(1)求证:AD=AE.
(2)若BE∥AC,试判断△ABC的形状,并说明理由.
分析:(1)由边角关系求证△ADB≌△AEB即可;
(2)由题中条件可得∠BAC=60°,进而可得△ABC为等边三角形.
(2)由题中条件可得∠BAC=60°,进而可得△ABC为等边三角形.
解答: 证明:(1)∵AB=AC,点D是BC的中点,
证明:(1)∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∵AE⊥AB,
∴∠E=90°=∠ADB,
∵AB平分∠DAE,
∴∠1=∠2,
在△ADB和△AEB中,
,
∴△ADB≌△AEB(AAS),
∴AD=AE;
(2)△ABC是等边三角形.理由:
∵BE∥AC,
∴∠EAC=90°,
∵AB=AC,点D是BC的中点,
∴∠1=∠2=∠3=30°,
∴∠BAC=∠1+∠3=60°,
∴△ABC是等边三角形.
 证明:(1)∵AB=AC,点D是BC的中点,
证明:(1)∵AB=AC,点D是BC的中点,∴AD⊥BC,
∴∠ADB=90°,
∵AE⊥AB,
∴∠E=90°=∠ADB,
∵AB平分∠DAE,
∴∠1=∠2,
在△ADB和△AEB中,
|
∴△ADB≌△AEB(AAS),
∴AD=AE;
(2)△ABC是等边三角形.理由:
∵BE∥AC,
∴∠EAC=90°,
∵AB=AC,点D是BC的中点,
∴∠1=∠2=∠3=30°,
∴∠BAC=∠1+∠3=60°,
∴△ABC是等边三角形.
点评:本题主要考查了全等三角形的判定及性质以及等边三角形的判定问题,能够熟练掌握.

练习册系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.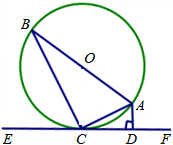 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.