题目内容
(2012•莱芜)如图1,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图2).
ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图2).
(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,试求旋转角α的度数.
 ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图2).
ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图2).(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,试求旋转角α的度数.
分析:(1)由于AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点,则AD=AE=
AB,再根据旋转的性质得到∠B′AD=∠C′AE=α,AB′=AB,AC′=AC,则AB′=AC′,根据三角形全等的判定方法可得到△B′AD≌△C′AE(SAS),则有DB′=EC′;
(2)由于DB′∥AE,根据平行线的性质得到∠B′DA=∠DAE=90°,又因为AD=
AB=
AB′,根据含30°的直角三角形三边的关系得到∠AB′D=30°,利用互余即可得到旋转角∠B′AD的度数.
| 1 |
| 2 |
(2)由于DB′∥AE,根据平行线的性质得到∠B′DA=∠DAE=90°,又因为AD=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)DB′=EC′.理由如下:
∵AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点,
∴AD=AE=
AB,
∵△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′,
∴∠B′AD=∠C′AE=α,AB′=AB,AC′=AC,
∴AB′=AC′,
在△B′AD和△C′AE中,
∵
,
∴△B′AD≌△C′AE(SAS),
∴DB′=EC′;
(2)∵DB′∥AE,
∴∠B′DA=∠DAE=90°,
在Rt△B′DA中,
∵AD=
AB=
AB′,
∴∠AB′D=30°,
∴∠B′AD=90°-30°=60°,
即旋转角α的度数为60°.
∵AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点,
∴AD=AE=
| 1 |
| 2 |
∵△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′,
∴∠B′AD=∠C′AE=α,AB′=AB,AC′=AC,
∴AB′=AC′,
在△B′AD和△C′AE中,
∵
|
∴△B′AD≌△C′AE(SAS),
∴DB′=EC′;
(2)∵DB′∥AE,
∴∠B′DA=∠DAE=90°,
在Rt△B′DA中,
∵AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AB′D=30°,
∴∠B′AD=90°-30°=60°,
即旋转角α的度数为60°.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点与旋转中心的连线段的夹角都等于旋转角.也考查了等腰三角形的性质、全等三角形的判定与性质以及含30°的直角三角形三边的关系.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 (2012•莱芜)如图,在数轴上点A表示的数可能是( )
(2012•莱芜)如图,在数轴上点A表示的数可能是( ) (2012•莱芜)如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是( )
(2012•莱芜)如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是( )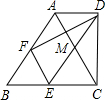 (2012•莱芜)如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,则下列结论不正确的是( )
(2012•莱芜)如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,则下列结论不正确的是( )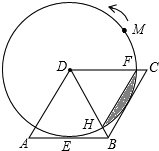 (2012•莱芜)如图,在菱形ABCD中,AB=2
(2012•莱芜)如图,在菱形ABCD中,AB=2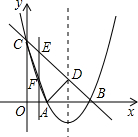 、B两点.
、B两点.