题目内容
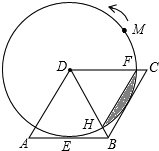 (2012•莱芜)如图,在菱形ABCD中,AB=2
(2012•莱芜)如图,在菱形ABCD中,AB=2| 3 |
(1)求证:⊙D与边BC也相切;
(2)设⊙D与BD相交于点H,与边CD相交于点F,连接HF,求图中阴影部分的面积(结果保留π);
(3)⊙D上一动点M从点F出发,按逆时针方向运动半周,当S△HDF=
| 3 |
分析:(1)过D作DQ⊥BC于Q,连接DE,根据切线性质得出DE⊥AB,根据菱形性质求出BD平分∠ABC,根据角平分线性质得出DE=DQ,根据切线判定推出即可;
(2)根据菱形性质和等边三角形判定得出等边三角形ADB,求出DE值,即可得出圆的半径长,得出等边三角形DCB和等边三角形DHF,求出△DFH的高FN,求出△DFH的面积和扇形FDH的面积,相减即可得出答案;
(3)根据△FDH的面积和已知求出△MDF边DF上的高MZ,求出∠MDF,同理得出另一点M′也符合,且圆心角是150°,根据弧长公式求出即可.
(2)根据菱形性质和等边三角形判定得出等边三角形ADB,求出DE值,即可得出圆的半径长,得出等边三角形DCB和等边三角形DHF,求出△DFH的高FN,求出△DFH的面积和扇形FDH的面积,相减即可得出答案;
(3)根据△FDH的面积和已知求出△MDF边DF上的高MZ,求出∠MDF,同理得出另一点M′也符合,且圆心角是150°,根据弧长公式求出即可.
解答: (1)证明:过D作DQ⊥BC于Q,连接DE,
(1)证明:过D作DQ⊥BC于Q,连接DE,
∵⊙D切AB于E,
∴DE⊥AB,
∵四边形ABCD是菱形,
∴BD平分∠ABC,
∴DE=DQ(角平分线性质),
∵DQ⊥BC,
∴⊙D与边BC也相切;
(2)解:过F作FN⊥DH于N,
∵四边形ABCD是菱形,
∴AD=AB=2
,
∵∠A=60°,
∴△ABD是等边三角形,
∴∠DBA=60°,DC∥AB,AD=BD=AB=2
∵DE⊥AB,
∴AE=BE=
,
由勾股定理得:DE=3=DH=DF,
∵四边形ABCD是菱形,
∴∠C=∠A=60°,DC=BC,
∴△DCB是等边三角形,
∴∠CDB=60°,
∵DF=DH,
∴△DFH是等边三角形,
∵FN⊥DH,
∴DN=NH=
,
由勾股定理得:FN=
,
∴S阴影=S扇形FDH-S△FDH=
-
×3×
=
π-
;
(3)解:过M作MZ⊥DF于Z,
∵由(2)知:S△HDF=
×3×
=
,DF=3,
又∵S△HDF=
S△DFM,
∴
=
×
×3×MZ,
∴MZ=
,
在Rt△DMZ中,sin∠MDZ=
=
,
∴∠MDZ=30°,
同理还有另一点M′也符合,此时MM′∥CD,∠M′DC=180°-30°=150°,
∴弧MF的长是
=
π;
弧FM′的长是
=
π.
答:动点M经过的弧长是
π或
π.
 (1)证明:过D作DQ⊥BC于Q,连接DE,
(1)证明:过D作DQ⊥BC于Q,连接DE,∵⊙D切AB于E,
∴DE⊥AB,
∵四边形ABCD是菱形,
∴BD平分∠ABC,
∴DE=DQ(角平分线性质),
∵DQ⊥BC,
∴⊙D与边BC也相切;
(2)解:过F作FN⊥DH于N,
∵四边形ABCD是菱形,
∴AD=AB=2
| 3 |
∵∠A=60°,
∴△ABD是等边三角形,
∴∠DBA=60°,DC∥AB,AD=BD=AB=2
| 3 |
∵DE⊥AB,
∴AE=BE=
| 3 |
由勾股定理得:DE=3=DH=DF,
∵四边形ABCD是菱形,
∴∠C=∠A=60°,DC=BC,
∴△DCB是等边三角形,
∴∠CDB=60°,
∵DF=DH,
∴△DFH是等边三角形,
∵FN⊥DH,
∴DN=NH=
| 3 |
| 2 |
由勾股定理得:FN=
3
| ||
| 2 |
∴S阴影=S扇形FDH-S△FDH=
| 60π×32 |
| 360 |
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
9
| ||
| 4 |
(3)解:过M作MZ⊥DF于Z,

∵由(2)知:S△HDF=
| 1 |
| 2 |
3
| ||
| 2 |
9
| ||
| 4 |
又∵S△HDF=
| 3 |
∴
9
| ||
| 4 |
| 3 |
| 1 |
| 2 |
∴MZ=
| 3 |
| 2 |
在Rt△DMZ中,sin∠MDZ=
| MZ |
| DM |
| 1 |
| 2 |
∴∠MDZ=30°,
同理还有另一点M′也符合,此时MM′∥CD,∠M′DC=180°-30°=150°,
∴弧MF的长是
| 30π×3 |
| 180 |
| 1 |
| 2 |
弧FM′的长是
| 150π×3 |
| 180 |
| 5 |
| 2 |
答:动点M经过的弧长是
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查的知识点是三角形的面积,等边三角形的性质和判定,勾股定理,菱形的性质,扇形的面积,锐角三角函数的定义,弧长公式等,主要考查学生综合运用性质进行推理和计算的能力,题目综合性比较强,难度偏大.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 (2012•莱芜)如图,在数轴上点A表示的数可能是( )
(2012•莱芜)如图,在数轴上点A表示的数可能是( ) (2012•莱芜)如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是( )
(2012•莱芜)如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是( )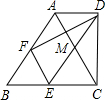 (2012•莱芜)如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,则下列结论不正确的是( )
(2012•莱芜)如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,则下列结论不正确的是( )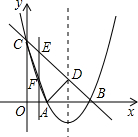 、B两点.
、B两点.