题目内容
【题目】（本题满分10分）抛物线
与x轴交与
，
两点，
（1）求该抛物线的解析式；
（2）设（1）中的抛物线与y轴交于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．
【答案】（1）y=-x2-2x+3；（2）存在Q（-1，2）.
【解析】试题分析：（1）把A（1,0）B（-3，0）代入
然后解方程组即可；（2）因为线段AC的长固定不变，所以当AQ+CQ的长最小时△QAC的周长最小，根据轴对称的性质可知直线BC与对称轴的交点即为Q点，用待定系数法求直线BC解析式，把对称轴x=-1代入即可.
试题解析：解（1）把A（1,0）B（-3，0）代入到
3分
∴抛物线的解析式为y=-x2-2x+3 5分
（2）存在。 6分
过B、C作直线BC与对称轴x=-1的交点就是Q点，
设直线BC解析式为y=kx+b，把B（-3,0）C（0,3）代入到
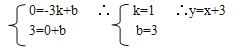
令XQ="-1" 得YQ=2 ∴Q（-1，2） 10分
练习册系列答案
相关题目
【题目】某中学在举行“弘扬中华传统文化读书月”活动结束后，对八年级（1）班40位学生所阅读书籍数量情况的统计结果如表所示：
阅读书籍数量（单位：本） | 1 | 2 | 3 | 3以上 |
人数（单位：人） | 12 | 16 | 9 | 3 |
这组数据的中位数和众数分别是（ ）
A. 2，2B. 1，2C. 3，2D. 2，1
