题目内容
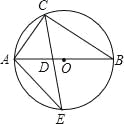
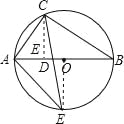
【题目】如图，△ABC内接于⊙O，AB是⊙O的直径，∠B=30°，CE平分∠ACB交⊙O于E，交AB于点D，连接AE，则S△ADE：S△CDB的值等于（ ）
A. 1：
B. 1：
C. 1：2 D. 2：3
【答案】D
【解析】试题分析：由AB是⊙O的直径，得到∠ACB=90°，根据已知条件得到
，根据三角形的角平分线定理得到
，求出AD=
AB，BD=
AB，过C作CE⊥AB于E，连接OE，由CE平分∠ACB交⊙O于E，得到OE⊥AB，求出OE=
AB，CE=
AB，根据三角形的面积公式即可得到结论．
∵AB是⊙O的直径， ∴∠ACB=90°，∵∠B=30°，∴，
∵CE平分∠ACB交⊙O于E，∴，∴AD=AB，BD=AB，
过C作CE⊥AB于E，连接OE，∵CE平分∠ACB交⊙O于E，∴
=
，
∴OE⊥AB，∴OE=AB，CE=AB，
∴S△ADE：S△CDB=（AD`OE）：（BD`CE）=（×AB·AB）：（×AB·AB）=2：3．
练习册系列答案
相关题目
