题目内容
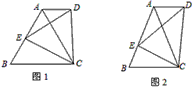
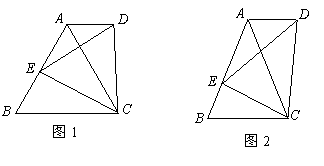
探究一:如图1,正△ABC中,E为AB边上任一点,△CDE为正三角形,连结AD,猜想AD与BC的位置关系,并说明理由.
探究二:如图2,若△ABC为任意等腰三角形,AB=AC,E为AB上任一点,△CDE为等腰三角形,DE=DC,且∠BAC=∠EDC,连接AD,猜想AD与BC的位置关系,并说明理由.
 |
解(1)![]()

![]() 与
与![]() 为正三角形
为正三角形
![]()
![]()
![]()
在![]() 与
与![]() 中
中

![]()
![]()
![]()
![]()
 (2)
(2)![]()
![]() 与
与![]() 为等腰三角形,且∠BAC=∠EDC
为等腰三角形,且∠BAC=∠EDC
![]()
![]()
![]() 即
即![]()
![]()
![]()
![]() 又
又![]()
![]()
![]()
![]()

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
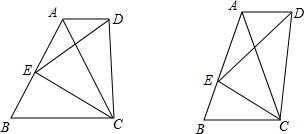 (2011•路北区一模)探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.
(2011•路北区一模)探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.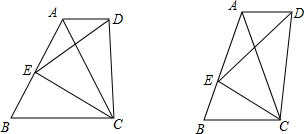 探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.
探究一:如图,正△ABC中,E为AB边上任一点,△CDE为正三角形,连接AD,猜想AD与BC的位置关系,并说明理由.