题目内容
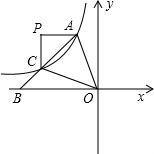 如图,C为AB的中点,PA∥x轴,PC∥y轴,且S四边形PAOC=4,双曲线
如图,C为AB的中点,PA∥x轴,PC∥y轴,且S四边形PAOC=4,双曲线 过A,C两点,那么k=________.
过A,C两点,那么k=________.
-4
分析:设点A,B,C,分别求出各点之间的关系,代入四边形的面积公式中求出k的值即可.
解答:设A(x1,y1),C(x2,y2),B(x3,0)则P(x2,y1)
∵双曲线 过A,C两点
过A,C两点
∴A(x1,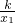 ),C(x2,
),C(x2,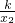 )
)
又∵C为AB的中点,即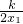 =
=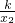 ,
, ×(x1+x3)=x2
×(x1+x3)=x2
∴x2=2x1,x3=3x1
S四边形PAOC=|x2|×|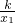 |-
|- ×|x2|×|
×|x2|×|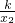 |-
|- ×|x1|×|
×|x1|×|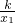 |=4
|=4
即:|k|=4
又∵双曲线 的图形在第二象限,故k<0
的图形在第二象限,故k<0
∴k=-4.
故答案为:-4.
点评:本题主要考查利用面积互补来计算相交双曲线的常数值.同学们要熟练掌握这种方法.
分析:设点A,B,C,分别求出各点之间的关系,代入四边形的面积公式中求出k的值即可.
解答:设A(x1,y1),C(x2,y2),B(x3,0)则P(x2,y1)
∵双曲线
 过A,C两点
过A,C两点∴A(x1,
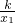 ),C(x2,
),C(x2,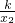 )
)又∵C为AB的中点,即
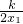 =
=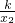 ,
, ×(x1+x3)=x2
×(x1+x3)=x2∴x2=2x1,x3=3x1
S四边形PAOC=|x2|×|
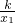 |-
|- ×|x2|×|
×|x2|×|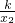 |-
|- ×|x1|×|
×|x1|×|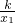 |=4
|=4即:|k|=4
又∵双曲线
 的图形在第二象限,故k<0
的图形在第二象限,故k<0∴k=-4.
故答案为:-4.
点评:本题主要考查利用面积互补来计算相交双曲线的常数值.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
 如图,C为AB的中点,PA∥x轴,PC∥y轴,且S四边形PAOC=4,双曲线
如图,C为AB的中点,PA∥x轴,PC∥y轴,且S四边形PAOC=4,双曲线
 (2012•徐州)如图,C为AB的中点.四边形ACDE为平行四边形,BE与CD相交于点F.
(2012•徐州)如图,C为AB的中点.四边形ACDE为平行四边形,BE与CD相交于点F. 如图,D为AB的中点,点E在AC上,将△ABC沿DE折叠,使点A落在BC边上的点F处.求证:EF=EC.
如图,D为AB的中点,点E在AC上,将△ABC沿DE折叠,使点A落在BC边上的点F处.求证:EF=EC.