题目内容
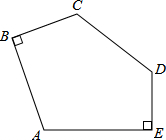 如图,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,则五边形ABCDE的面积为
如图,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,则五边形ABCDE的面积为考点:全等三角形的判定与性质
专题:计算题
分析:延长DE到F,使EF=BC,连接AC,AD,AF,利用SAS得到三角形ABC与三角形AEF全等,利用全等三角形的对应边相等得到AC=AF,根据CD=BC+DE,EF=BC,等量代换得到CD=DF,利用SSS得到三角形ACD与三角形AFD全等,根据三角形ABC与三角形AEF全等,得到五边形ABCDE等于三角形ADF的2倍,求出即可.
解答: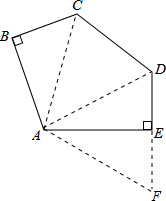 解:延长DE到F,使EF=BC,连接AC,AD,AF,
解:延长DE到F,使EF=BC,连接AC,AD,AF,
在△ABC和△AEF中,
,
∴△ABC≌△AEF(SAS),
∴AC=AF,
∵CD=BC+DE,EF=BC,
∴CD=DF,
在△ACD和△AFD中,
,
∴△ACD≌△AFD(SSS),
∵△ABC≌△AEF,
∴S△ABC=S△AEF,
∴S五边形ABCDE=S△ABC+S四边形AEDC=S△AEF+S四边形AEDC=2S△ADF,
∵AB=CD=AE=2,∠AED=90°,
∴S△ADF=2,
则S五边形ABCDE=4.
故答案为:4
 解:延长DE到F,使EF=BC,连接AC,AD,AF,
解:延长DE到F,使EF=BC,连接AC,AD,AF,在△ABC和△AEF中,
|
∴△ABC≌△AEF(SAS),
∴AC=AF,
∵CD=BC+DE,EF=BC,
∴CD=DF,
在△ACD和△AFD中,
|
∴△ACD≌△AFD(SSS),
∵△ABC≌△AEF,
∴S△ABC=S△AEF,
∴S五边形ABCDE=S△ABC+S四边形AEDC=S△AEF+S四边形AEDC=2S△ADF,
∵AB=CD=AE=2,∠AED=90°,
∴S△ADF=2,
则S五边形ABCDE=4.
故答案为:4
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
余姚某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据(单位:分):10、12、15、8、16、18、19、18、20、18、18、20、28、22、25、20、15、16、21、16.若将这些数据以4分为组距进行分组,则组数是( )
| A、4组 | B、5组 | C、6组 | D、7组 |
 如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个长方形的两边长(x>y),观察图案及以下关系式:①x-y=n;②xy=
如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个长方形的两边长(x>y),观察图案及以下关系式:①x-y=n;②xy=