题目内容
11.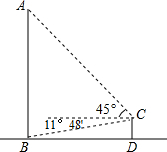 全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为11°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为58米(参考数据:tan78°12′≈4.8).
全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为11°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为58米(参考数据:tan78°12′≈4.8).
分析 直接利用锐角三角函数关系得出EC的长,进而得出AE的长,进而得出答案.
解答  解:如图所示:过C作CE⊥AB于点E,
解:如图所示:过C作CE⊥AB于点E,
∵∠CDB=90°,∠EBD=90°,
∴四边形EBDC是矩形,
∴BE=DC,
∵∠ECB=11°48′,
∴∠EBC=78°12′,
则tan78°12′=$\frac{EC}{BE}$=$\frac{EC}{10}$=4.8,
解得:EC=48(m),
∵∠AEC=45°,则AE=EC,且BE=DC=10m,
∴此塑像的高AB约为:AE+EB=58(米).
故答案为:58.
点评 此题主要考查了解直角三角形的应用,根据题意得出EC的长是解题关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
2.我国建造的长江三峡水电站,估计总装机容量达16780000千瓦,16780000用科学记数法表示为( )
| A. | 16.7×106 | B. | 1.68×107 | C. | 1.678×107 | D. | 1.678×108 |
16.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A(1,a)、B(3,b),则a与b的关系正确的是( )
| A. | a=b | B. | a=-b | C. | a<b | D. | a>b |
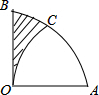 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.
如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.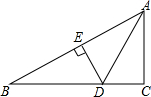 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( ) 把一个正六棱柱如图1摆放,光线由上向下照射此正六棱柱时的正投影是( )
把一个正六棱柱如图1摆放,光线由上向下照射此正六棱柱时的正投影是( )


