题目内容
如图，已知A是双曲线
（x＞0）上一点，过点A作AB∥x轴，交双曲线
（x＜0）于点B，若OA⊥OB，则
= ．
【答案】分析：首先根据A、B点所在位置设出A、B两点的坐标，再利用勾股定理表示出AO2，BO2以及AB的长，再表示出
，进而可得到
．
解答：解：∵A点在双曲线
（x＞0）上一点，
∴设A（
，m），
∵AB∥x轴，B在双曲线
（x＜0）上，
∴设B（-
，m），
∴OA2=
+m2，BO2=
+m2，
∵OA⊥OB，
∴OA2+BO2=AB2，
∴
+m2+
+m2=（
+
）2，
∴m2=
，
∴
=
=
=
，
∴
=
，
故答案为：
．
点评：此题主要考查了反比例函数图象上点的坐标特点，以及勾股定理的应用，关键是表示出A、B两点的坐标．
，进而可得到．解答：解：∵A点在双曲线
（x＞0）上一点，∴设A（
，m），∵AB∥x轴，B在双曲线
（x＜0）上，∴设B（-
，m），∴OA2=
+m2，BO2=+m2，∵OA⊥OB，
∴OA2+BO2=AB2，
∴
+m2++m2=（+）2，∴m2=
，∴
===，∴
=，故答案为：
．点评：此题主要考查了反比例函数图象上点的坐标特点，以及勾股定理的应用，关键是表示出A、B两点的坐标．
练习册系列答案
相关题目
（2012•宝安区二模）如图，已知A是双曲线
与双曲线
交于点
．
，
的值；
，在
轴的正半轴上是否存在点
，使
是等腰三角形？若存在，请直接写出所有符合条件的点
的坐标；若不存在，请说明理由．
如图，已知A是双曲线
（x＞0）上一点，过点A作AB∥x轴，交双曲线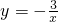
（x＜0）于点B，若OA⊥OB，则
=________．
（x＞0）上一点，过点A作AB∥x轴，交双曲线
（x＜0）于点B，若OA⊥OB，则
= ．