题目内容
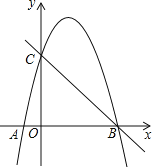
【题目】在平面直角坐标系中，抛物线
如图所示.已知点A的坐标为（1，-1），过点A作
轴交抛物线于点
，过点作
交抛物线于点
，过点作
轴交抛物线于点
，过点作
交抛物线于点
，……，依次进行下去，则点
的坐标为（ ）
A.（1010，-10102）B.（-1010，-10102）C.（1009，-10092）D.（-1009，-10092）
【答案】B
【解析】
根据二次函数的对称性求出
的坐标，然后由
，则k相等，可求出
解析式，与抛物线联立可求
，以此类推，根据坐标的变化找出规律，得到
.
A的坐标为（1，-1）, 
轴，根据对称性可得
，
设OA直线解析式y=kx，代入（1，-1）得k=-1，又因为，所以两直线k相等，
设解析式为y=-x+b，代入，得，1+b=-1，∴b=-2，则：y=-x-2,
与抛物线联立得
，解得
或
，∴
同理可得
，
：
，
…，
以此类推
，
…
，
所以
，故选B.
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
