题目内容
如图，D为⊙O的直径AB上任一点，CD⊥AB，若AD、BD的长分别等于a和b，则通过比较线段OC与CD的大小，可以得到关于正数a和b的一个性质，你认为这个性质是
- A.
- B.
- C.
- D.
A
分析：连接AC，BC；根据射影定理求解．
解答：
解：连接AC，BC．
根据AB是直径，因而∠ACB是直角，CD是直角三角形斜边上的高线，因而CD2=AD•DB，即CD2=ab，CD=
．
而OC=
，并且OC≥CD，则≥．
故选A．
点评：本题主要考查了圆中直径所对的弦是直径，并且考查了垂径定理．
分析：连接AC，BC；根据射影定理求解．
解答：
解：连接AC，BC．根据AB是直径，因而∠ACB是直角，CD是直角三角形斜边上的高线，因而CD2=AD•DB，即CD2=ab，CD=
．而OC=
，并且OC≥CD，则≥．故选A．
点评：本题主要考查了圆中直径所对的弦是直径，并且考查了垂径定理．
练习册系列答案
相关题目
25、如图：AB为⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠DCB=∠A．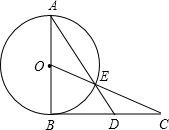
如图，AB为⊙O的直径，过点B作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D．
5、如图，AB为⊙O的直径，点C在⊙O上．若∠C=16°，则∠BOC的度数是（ ）
（2012•安溪县质检）如图，AB为⊙O的直径，CD为弦，且CD⊥AB于点E，下列结论：①CE=ED；②OE=EB；③AC=AD；④AC=CD．其中正确结论的序号是
如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过△ABC的内切圆圆心O，且点E在半圆弧上．①若正方形的顶点F也在半圆弧上，则半圆的半径与正方形边长的比是