题目内容
 如图,一张宽3cm,长为4cm的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则ME的长为________cm.
如图,一张宽3cm,长为4cm的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则ME的长为________cm.
- A.2
- B.

- C.

- D.

D
分析:依题意可知△DEM为直角三角形,且DM= AD=2,由折叠的性质可证△ABG≌△C′DG,在Rt△ABG中,由勾股定理求BG,利用△ABG∽△MDE,可得对应边的比相等可求ME.
AD=2,由折叠的性质可证△ABG≌△C′DG,在Rt△ABG中,由勾股定理求BG,利用△ABG∽△MDE,可得对应边的比相等可求ME.
解答: 解:如图,由已知可得EN垂直平分AD,DM=
解:如图,由已知可得EN垂直平分AD,DM= AD=2,
AD=2,
∵AB=CD=C′D,∠A=∠C′=90°,∠AGB=∠C′GD,
∴△ABG≌△C′DG,
设AG=x,则BG=GD=4-x,
在Rt△ABG中,由勾股定理得
AB2+AG2=BG2,即32+x2=(4-x)2,
解得x= ,易证△ABG∽△MDE,
,易证△ABG∽△MDE,
∴ =
= ,即
,即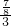 =
= ,解得ME=
,解得ME= .
.
故选D.
点评:本题考查了折叠的性质,三角形全等的判定与性质,三角形相似的判定与性质,勾股定理的运用.关键是由性质将有关线段进行转化.
分析:依题意可知△DEM为直角三角形,且DM=
 AD=2,由折叠的性质可证△ABG≌△C′DG,在Rt△ABG中,由勾股定理求BG,利用△ABG∽△MDE,可得对应边的比相等可求ME.
AD=2,由折叠的性质可证△ABG≌△C′DG,在Rt△ABG中,由勾股定理求BG,利用△ABG∽△MDE,可得对应边的比相等可求ME.解答:
 解:如图,由已知可得EN垂直平分AD,DM=
解:如图,由已知可得EN垂直平分AD,DM= AD=2,
AD=2,∵AB=CD=C′D,∠A=∠C′=90°,∠AGB=∠C′GD,
∴△ABG≌△C′DG,
设AG=x,则BG=GD=4-x,
在Rt△ABG中,由勾股定理得
AB2+AG2=BG2,即32+x2=(4-x)2,
解得x=
 ,易证△ABG∽△MDE,
,易证△ABG∽△MDE,∴
 =
= ,即
,即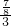 =
= ,解得ME=
,解得ME= .
.故选D.
点评:本题考查了折叠的性质,三角形全等的判定与性质,三角形相似的判定与性质,勾股定理的运用.关键是由性质将有关线段进行转化.

练习册系列答案
相关题目
 如图,一张宽3cm,长为4cm的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则ME的长为( )cm.
如图,一张宽3cm,长为4cm的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则ME的长为( )cm. 如图,一张长为10cm,宽为
如图,一张长为10cm,宽为 如图,一张矩形纸片ABCD的长AD=9cm,宽AB=3cm,现将其折叠,使点D与点B重合,则BE=
如图,一张矩形纸片ABCD的长AD=9cm,宽AB=3cm,现将其折叠,使点D与点B重合,则BE=


