题目内容
6.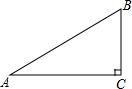 如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是$\frac{4}{5}$.
如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是$\frac{4}{5}$.
分析 先利用勾股定理求出AC的长,再根据锐角的余弦等于邻边比斜边求解即可.
解答 解:∵在△ABC中,∠C=90°,AB=5,BC=3,
∴AC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴cosA=$\frac{AC}{AB}$=$\frac{4}{5}$.
故答案为$\frac{4}{5}$.
点评 本题考查锐角三角函数的概念:在直角三角形中,正弦等于对边比斜边;余弦等于邻边比斜边;正切等于对边比邻边.也考查了勾股定理.

练习册系列答案
相关题目
14.9的平方根是( )
| A. | 81 | B. | 3 | C. | ±3 | D. | ±$\sqrt{3}$ |
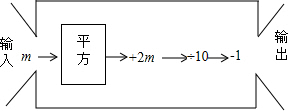
1.任意给定一个非零数,按下列程序计算,最后输出的结果是( )


| A. | m | B. | 2m | C. | m-1 | D. | 0 |
18.如果+2%表示增加2%,那么-6%表示( )
| A. | 增加14% | B. | 增加6% | C. | 减少26% | D. | 减少6% |
 如图,A、B、C是⊙O上的点,若∠AOB=70°,则∠ACB的度数为35°.
如图,A、B、C是⊙O上的点,若∠AOB=70°,则∠ACB的度数为35°.