题目内容
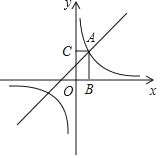
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() 顶点为
顶点为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的度数;
的度数;
![]() 若点
若点![]() 是线段
是线段![]() 上一个动点,过
上一个动点,过![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() .
.
①求线段![]() 的最大值;
的最大值;
②若![]() 是等腰三角形,直接写出
是等腰三角形,直接写出![]() 的值.
的值.

【答案】(1)y=x2-4x+3,(2)90°,(3)①![]() ,②m=2或m=
,②m=2或m=![]() 或m=1.
或m=1.
【解析】
(1)将点B,C代入抛物线的解析式中,利用待定系数法即可得出答案;
(2)先求出点D的坐标,然后利用OB=OC,得出∠CBO=45°,过D作DE⊥x 轴,垂足为E,再利用DE=BE,得出∠DBO=45°,则![]() 的度数可求;
的度数可求;
(3)①先用待定系数法求出直线BC的表达式,然后设出M,N的坐标,表示出线段MN的长度,利用二次函数的性质即可求出最大值;
②分三种情况: BN=BM, BN=MN, NM=BM分别建立方程求解即可.
解:(1)将点B(3,0)、C(0,3)代入抛物线y=x2+bx+c中,
得:![]() ,解得:
,解得:![]() .
.
故抛物线的解析式为y=x2-4x+3.
(2)y=x2-4x+3=(x-2)2-1,
∴D点坐标为(2,-1).
∵OB=OC=3,
∴∠CBO=45°,
过D作DE⊥x 轴,垂足为E,则DE=BE=1,
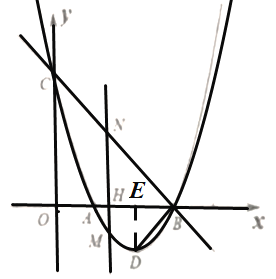
∴∠DBO=45°,
∴∠CBD=90°.
(3)①设直线BC的解析式为y=kx+3,得:0=3k+3,解得:k=-1,
∴直线BC的解析式为y=-x+3.
点M的坐标为(m,m2-4m+3),点N的坐标为(m,-m+3).
线段MN=(-m+3)-(m2-4m+3)=-m2+3m=-(m-![]() )2+
)2+![]() .
.
∴当m=![]() 时,线段MN取最大值,最大值为
时,线段MN取最大值,最大值为![]() .
.
②在Rt△NBH中,BH=3-m,BN=![]() (3-m).
(3-m).
当BN=BM时,NH=MH,则-m+3=-(m2-4m+3),
即m2-5m+6=0,解得m1=2,m2=3(舍去),
当BN=MN时,-m2+3m=![]() (3-m),解得:m1=
(3-m),解得:m1=![]() ,m2=3(舍去),
,m2=3(舍去),
当NM=BM时,∠MNB=∠NBM=45°,则MB与x轴重合,点M与点A重合,
∴m=1,
综合得:m=2或m=![]() 或m=1.
或m=1.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
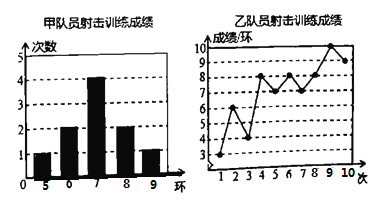
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)写出表格中![]() 的值:
的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | 1 |
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.