题目内容
已知：△ABC≌△A′B′C′，AB=5，BC=7，AD⊥BC于D，且AD=4，则A′B′上的高为
- A.4
- B.5
- C.6
- D.
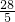
D
分析：分别作边AB，A′B′上的高CE，C′E′，然后根据三角形的面积公式即可求得CE的长，根据全等三角形的对应边上的高相等，即得到了A′B′上的高C′E′的长．
解答：
解：如图，分别作边AB，A′B′上的高CE，C′E′，
∵AB=5，BC=7，AD⊥BC于D，且AD=4，
∴S△ABC=
BC•AD=AB•CE，
∴CE=，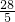
∵△ABC≌△A′B′C′，
∴CE=C′E′，
∴C′E′=．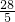
故选D．
点评：此题主要考查学生对全等三角形对应边上的高相等的理解及运用能力．
分析：分别作边AB，A′B′上的高CE，C′E′，然后根据三角形的面积公式即可求得CE的长，根据全等三角形的对应边上的高相等，即得到了A′B′上的高C′E′的长．
解答：
解：如图，分别作边AB，A′B′上的高CE，C′E′，∵AB=5，BC=7，AD⊥BC于D，且AD=4，
∴S△ABC=
BC•AD=AB•CE，∴CE=
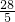，∵△ABC≌△A′B′C′，
∴CE=C′E′，
∴C′E′=
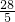．故选D．
点评：此题主要考查学生对全等三角形对应边上的高相等的理解及运用能力．
练习册系列答案
相关题目
20、已知直角△ABC中∠B=90°，延长BC到D，使CD=AB，过D作BD的垂线，在这个垂线上截取DE=BC．求证：AC⊥EC．
如图，已知三角形△ABC中，∠A=90°，AB=3，BC=6．
如图所示，已知在△ABC中，BC=4cm，把△ABC沿BC方向平移2cm得到△DEF．问：