题目内容
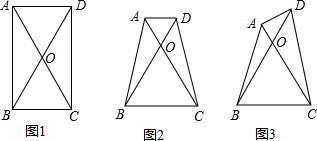
四边形ABCD是梯形，AD∥BC，已知AB=5，AD=3，CD=4| 2 |
| 4 |
| 5 |
分析：根据题意所述画出示意图，先求出AE、BE的长，然后利用勾股定理得出CF的长，进而可求出BC的长度．
解答：解：
①由题意得：AD=3，AB=5，CD=4
，sinB=
，
∴BE=ABcosB=5×
=3，AE=ABsinB=4，
在RT△DFC中，CF=
=
=4，
∴BC=BE+EF+CF=BE+AD+FC=10．
②
BE=ABcosB=5×
=3，AE=ABsinB=4，CF=
=
=4，
∴BC=BE+AD-FC=2．
故答案为：10或2．
①由题意得：AD=3，AB=5，CD=4
| 2 |
| 4 |
| 5 |
∴BE=ABcosB=5×
| 3 |
| 5 |
在RT△DFC中，CF=
| CD2-DF2 |
| CD2-AE2 |
∴BC=BE+EF+CF=BE+AD+FC=10．
②
BE=ABcosB=5×
| 3 |
| 5 |
| CD2-DF2 |
| CD2-AE2 |
∴BC=BE+AD-FC=2．
故答案为：10或2．
点评：本题考查了梯形的知识，难度一般，解答此类题目首先要画出示意图，这样对解题的帮助很大．
练习册系列答案
字词句段篇系列答案
相关题目
39、如图，已知四边形ABCD是梯形，你能用红笔画出图中任意一对同旁内角吗？图中共有几对同旁内角？
