题目内容
如图,四边形ABCD中,AC与BD相交于点O,AC=BD,∠BOC=60°.
(1)移动点A至如图1,四边形ABCD是平行四边形时(3)移动点A至如图2,四边形ABCD是梯形时,且AD∥BC,猜想并写出线段AC与线段AD、BC之间的关系,请证明你的结论;
(4)移动点A至如图3,四边形ABCD中,AD与BC不平行时,猜想并写出线段AC与线段AD、BC之间的关系,不必说明理由.
如图,四边形ABCD中,AC与BD相交于点O,AC=BD,∠BOC=60°.
(1)移动点A至如图1,四边形ABCD是平行四边形时,BC=5,试写出AC的长度;
(2)在(1)的条件下,求证:AC=AD+BC;
(3)移动点A至如图2,四边形ABCD是梯形时,且AD∥BC,猜想并写出线段AC与线段AD、BC之间的关系,请证明你的结论;
(4)移动点A至如图3,四边形ABCD中,AD与BC不平行时,猜想并写出线段AC与线段AD、BC之间的关系,不必说明理由.
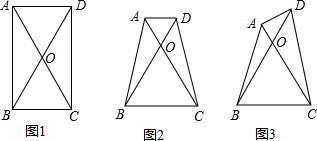
(1)移动点A至如图1,四边形ABCD是平行四边形时(3)移动点A至如图2,四边形ABCD是梯形时,且AD∥BC,猜想并写出线段AC与线段AD、BC之间的关系,请证明你的结论;
(4)移动点A至如图3,四边形ABCD中,AD与BC不平行时,猜想并写出线段AC与线段AD、BC之间的关系,不必说明理由.
如图,四边形ABCD中,AC与BD相交于点O,AC=BD,∠BOC=60°.
(1)移动点A至如图1,四边形ABCD是平行四边形时,BC=5,试写出AC的长度;
(2)在(1)的条件下,求证:AC=AD+BC;
(3)移动点A至如图2,四边形ABCD是梯形时,且AD∥BC,猜想并写出线段AC与线段AD、BC之间的关系,请证明你的结论;
(4)移动点A至如图3,四边形ABCD中,AD与BC不平行时,猜想并写出线段AC与线段AD、BC之间的关系,不必说明理由.

分析:(1)根据由条件根据四边形ABCD是平行四边形就可以得出四边形ABCD是矩形,再由矩形的性质就可以得出结论;
(2)根据矩形的性质及其他条件就可以得出△AOD,△BOC为等边三角形,由等边三角形的性质就可以得出结论;
(3)当四边形ABCD为等腰梯形时,三角形ABO和三角形CDO也是等边三角形,所以会有AB+CD=AC;
(2)根据矩形的性质及其他条件就可以得出△AOD,△BOC为等边三角形,由等边三角形的性质就可以得出结论;
(3)当四边形ABCD为等腰梯形时,三角形ABO和三角形CDO也是等边三角形,所以会有AB+CD=AC;
解答:解:(1)∵四边形ABCD是平行四边形,且AC=BD,
∴四边形ABCD是矩形,
∴OB=OC.AC=2OC
∵∠BOC=60°,
∴△BOC是等边三角形,
∴OC=BC=5,
∴AC=10;
(2)∵四边形ABCD是矩形,
∴AD=BC,AO=CO=
AC,BO=DO=
BD,
∵AC=BD,
∴AO=CO=BO=DO=
AC=
BD.
∵∠BOC=60°,
∴△AOD,△BOC为等边三角形,
∴AO=OC=BC=AD,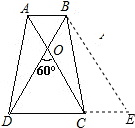
∵AC=AO+OC,
∴AC=AD+BC;
(3)AB+CD=AC;
∵四边形ABCD是梯形,AC=BD,
∴梯形ABCD是等腰梯形,
过B作AC的平行线,交DC的延长线于点E.则四边形ACEB是平行四边形,
∴AC=BE=BD,
∴∠BDC=∠E,∠E=∠ACD
∴∠BDC=∠ACD
又∵∠DOC=60°,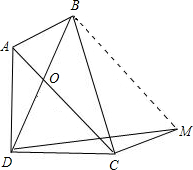
∴△DOC都是正三角形,
同理:△AOB是等边三角形.
∴OA=OB=AB,OD=OC=DC
即AB+CD=AO+C0=AC;
(3)不成立,应为AB+CD>AC.
如图所示过B作BM∥AC,过C作CM∥AB,
则四边形ABMC为平行四边形,
∴CM=AB,BM=AC=BD,BM∥AC,
∵∠DOC=60°,
∴∠DBM=∠DOC=60°
∴三角形DBM为等边三角形,
∴BM=AC=DM
在△CDM中,CM+CD>DM,
即AB+CD>AC.
∴四边形ABCD是矩形,
∴OB=OC.AC=2OC
∵∠BOC=60°,
∴△BOC是等边三角形,
∴OC=BC=5,
∴AC=10;
(2)∵四边形ABCD是矩形,
∴AD=BC,AO=CO=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC=BD,
∴AO=CO=BO=DO=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BOC=60°,
∴△AOD,△BOC为等边三角形,
∴AO=OC=BC=AD,

∵AC=AO+OC,
∴AC=AD+BC;
(3)AB+CD=AC;
∵四边形ABCD是梯形,AC=BD,
∴梯形ABCD是等腰梯形,
过B作AC的平行线,交DC的延长线于点E.则四边形ACEB是平行四边形,
∴AC=BE=BD,
∴∠BDC=∠E,∠E=∠ACD
∴∠BDC=∠ACD
又∵∠DOC=60°,

∴△DOC都是正三角形,
同理:△AOB是等边三角形.
∴OA=OB=AB,OD=OC=DC
即AB+CD=AO+C0=AC;
(3)不成立,应为AB+CD>AC.
如图所示过B作BM∥AC,过C作CM∥AB,
则四边形ABMC为平行四边形,
∴CM=AB,BM=AC=BD,BM∥AC,
∵∠DOC=60°,
∴∠DBM=∠DOC=60°
∴三角形DBM为等边三角形,
∴BM=AC=DM
在△CDM中,CM+CD>DM,
即AB+CD>AC.
点评:本题考查了平行四边形的性质的运用、矩形的性质的运用、等腰梯形的基本性质的运用,等边三角形的性质的运用,解答本题时灵活运用等边三角形的性质是关键.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.