题目内容
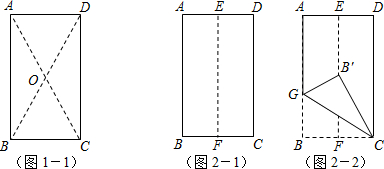
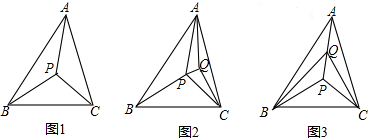
在如图一、图二、图三中，分别是由1个、2个、n个正方形连接成的图形．在图1中，x=70°；在图二中，y=28°；通过（1）、（2）的计算，请写出图三中a+b+c+…+d与n的数量关系式______．
解：如图，连接各小正方形的对角线，图一中，61°+119°+20°+x+45°×2=360°，
所以，20°+x=360°-61°-119°-45°×2=90°，
图二中，61°+119°+31°+121°+45°×4+y=（5-2）•180°，
所以，31°+121°+y=540°-61°-119°-45°×4=180°，
…，
依此类推，a+b+c+…+d=（n+1+2-2）•180°-45°×2n-61°-119°=90°n．
故答案为：90°n．
分析：连接各小正方形的对角线，然后根据正方形的对角线平分一组对角，多边形的内角和公式分别列式求出右边几个角的度数的和，从而找出变化规律即可得解．
点评：本题考查了多边形的内角和公式，正方形的对角线平分一组对角的性质，作辅助线构造出多边形是解题的关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
；
