题目内容
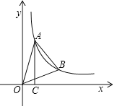
【题目】在Rt△ABC中,∠ACB=90°,AC=15,AB=25,点D为斜边AB上动点.

(1)如图1,当CD⊥AB时,求CD的长度;
(2)如图2,当AD=AC时,过点D作DE⊥AB交BC于点E,求CE的长度;
(3)如图3,在点D的运动过程中,连接CD,当△ACD为等腰三角形时,直接写出AD的长度.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当△ACD为等腰三角形时,AD的长度为:15或18或
;(3)当△ACD为等腰三角形时,AD的长度为:15或18或![]() .
.
【解析】
(1)由勾股定理求出BC的长度,再由面积法求出CD的长度即可;
(2)连接AE,可证明△ACE≌△ADE,得到CE=DE,设CE=DE=x,则BE=![]() ,由BD=10,则利用勾股定理,求出x,即可得到CE的长度;
,由BD=10,则利用勾股定理,求出x,即可得到CE的长度;
(3)当△ACD为等腰三角形时,可分为三种情况进行①AD=AC;②AC=CD;③AD=CD;对三种情况进行计算,即可得到AD的长度.
解:(1)如图,
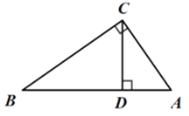
在Rt△ABC中,∠ACB=90°,AC=15,AB=25,
∴BC=![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ;
;
(2)如图,连接AE,
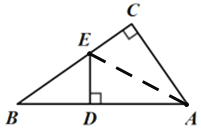
∵DE⊥AB,
∴∠ADE=∠C=90°,
在Rt△ADE和Rt△ACE中,
![]() ,
,
∴Rt△ADE≌Rt△ACE,
∴DE=CE;
设DE=CE=x,则BE=![]() ,又BD=
,又BD=![]()
在Rt△BDE中,由勾股定理,得
![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(3)在Rt△ABC中,有AB=25,AC=15,BC=20,点C到AB的距离为12;
当△ACD为等腰三角形时,可分为三种情况:
①当AD=AC时,AD=15;
②当AC=CD时,如图,作CE⊥AB于点E,则![]() ,
,
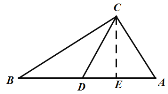
∵CE=12,由勾股定理,得
![]() ,
,
∴![]() ;
;
③当AD=CD时,如图,

在Rt△ABC中,∠ACB=90°,
当点D是AB中点时,有AD=BD=CD,
∴![]() ;
;
综合上述,当△ACD为等腰三角形时,AD的长度为:15或18或![]() .
.

练习册系列答案
相关题目