题目内容
【题目】如图,点![]() 、
、![]() 在反比例函数
在反比例函数![]() 的图象上,且点
的图象上,且点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]()
![]() .过点
.过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,且
,且![]() 的面积为
的面积为![]() .
.
![]() 求该反比例函数的解析式;
求该反比例函数的解析式;
![]() 若
若![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,当
,当![]() 满足什么条件,
满足什么条件,![]() ?
?
![]() 求
求![]() 的面积.
的面积.
【答案】![]()
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]()
![]() .
.
【解析】
(1)根据反比例函数k的几何意义得到![]() ,即可得到k=4,于是得到反比例函数解析式为
,即可得到k=4,于是得到反比例函数解析式为![]() ;
;
(2)当a=5时,![]() ,
,![]() ,然后观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
,然后观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
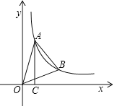
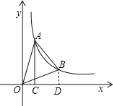
(3)过点B作BD⊥x轴,垂足为D,如图,根据反比例函数图象上点的坐标特征得![]() ,
,![]() ,由于S四边形AODB=S△AOC+S梯形ACDB=S△AOB+S△BOD,根据反比例函数k的几何意义得S△AOC=S△BOD,则S梯形ACDB=S△AOB,然后根据梯形公式计算即可.
,由于S四边形AODB=S△AOC+S梯形ACDB=S△AOB+S△BOD,根据反比例函数k的几何意义得S△AOC=S△BOD,则S梯形ACDB=S△AOB,然后根据梯形公式计算即可.
![]() ∵
∵![]() 轴,
轴,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴反比例函数解析式为![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,
故当![]() 时,
时,![]() ;
;
![]() 过点
过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,如图,
,如图,![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]()
![]() ,
,
∴![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目