题目内容
 如图,在六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=22,试求DE+EF的值.
如图,在六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=22,试求DE+EF的值.分析:分别作AB的延长线、CD的反向延长线交于G,作DE/AF的延长线交于H,可得到2个等边三角形,四边形AGDH是平行四边形,从而得出结论.
解答:解:分别作AB的延长线、CD的反向延长线交于G,作DE/AF的延长线交于H,
∵∠A=∠ABC=∠BCD=∠D=∠DEF=∠AFE,
∴∠A=∠ABC=∠BCD=∠D=∠AFE=∠DEF=120°,
∴∠GBC=∠BCG=∠HFE=∠HEF=60°,
∴△BCD、△HEF是等边三角形,
∴BC=BG,EF=EH,∠G=∠H═60°,
∴∠A+∠G=180°,∠D+∠G=180°,
∴AG∥DH,AH∥GD,
∴四边形AGDH是平行四边形,
∴AG=DH,
∴AB+BC=DE+EF=22.

∵∠A=∠ABC=∠BCD=∠D=∠DEF=∠AFE,
∴∠A=∠ABC=∠BCD=∠D=∠AFE=∠DEF=120°,
∴∠GBC=∠BCG=∠HFE=∠HEF=60°,
∴△BCD、△HEF是等边三角形,
∴BC=BG,EF=EH,∠G=∠H═60°,
∴∠A+∠G=180°,∠D+∠G=180°,
∴AG∥DH,AH∥GD,
∴四边形AGDH是平行四边形,
∴AG=DH,
∴AB+BC=DE+EF=22.
点评:此题主要考查了多边形内角与外角,等边三角形的性质,平行四边形的判定和性质,本题关键是证明△BCD、△HEF是等边三角形.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
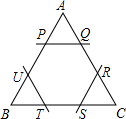 如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )
如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
 23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.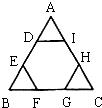 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是 如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为
如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为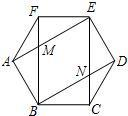 如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.