题目内容

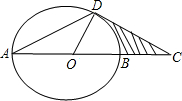
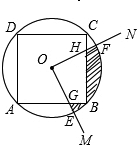
如图，在半径为2，圆心角等于90°的扇形AOB内部作一个直角梯形OBCD，使点C在
AB
上，且为
AB
的中点，D在OA上，则阴影部分的面积为（结果保留π）______．
连接OC，

∵点C为
AB
的中点，
∴∠AOC=∠BOC=45°，
∴△ODC是等腰直角三角形，
∵OC=2，
∴OD=CD=
2
，
则S阴影=S扇形-S梯形OBCD=
90π×22
360
-
1
2
（
2
+2）×
2
=π-1-
2
．
故答案为：π-1-
2
．
练习册系列答案
相关题目
如图，AB是⊙O的直径，C是⊙O上一点，CD⊥AB于D，且AB=8，DB=2．
（1）求证：△ABC∽△CBD；
（2）求图中阴影部分的面积．（结果精确到0.1，参考数据π≈3.14，
3
≈1.73）
如图，△ABC为等腰直角三角形，∠A=90°，AB=AC=
2
，⊙A与BC相切，则图中阴影部分的面积为（　　）
A．1-
π
2
B．1-
π
3
C．1-
π
4
D．1-
π
5
如图，有一住宅小区呈三角形ABC形状，且周长为2 000m，现规划沿小区周围铺上宽为3m的草坪，则草坪的面积（精确到1）是（　　）
A．6000m2B．6016m2C．6028m2D．6036m2
如图，在△OAB中，OA=OB=2，∠OAE=30°，⊙O切AB于E，且分别交OA、OB于C、D，求图中阴影部分的面积．
如图，半径为2的三个等圆两两相切于点A，B，C，则图中阴影部分的面积为（　　）
A．4
3
-
8
3
π		B．4
3
+
4
3
π		C．4
3
-
4
3
π		D．2
3
+
4
3
π
如图，依次以三角形、四边形、…、n边形的各顶点为圆心画半径为l的圆，且圆与圆之间两两不相交．把三角形与各圆重叠部分面积之和记为S3，四边形与各圆重叠部分面积之和记为S4，…．n边形与各圆重叠部分面积之和记为Sn．则S90的值为______．（结果保留π）
如图，⊙O的直径AB=6，D为⊙O上一点，∠BAD=30°，过D点的切线交AB的延长线于点C．阴影部分的面积为______．（精确到0.01）
如图，正方形ABCD内接于⊙O，⊙O的半径为2，以圆心O为顶点作∠MON，使∠MON=90°，OM、ON分别与⊙O交于点E、F，与正方形ABCD的边交于点G、H，则由OE、OF、
EF
及正方形ABCD的边围成的图形（阴影部分）的面积S=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网