题目内容
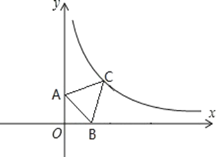
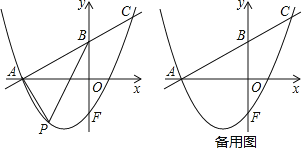
【题目】如图,已知在平面直角坐标系xOy中,直线y=![]() x+
x+![]() 与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=
与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=![]() x2+bx+c经过点A和点F,与直线AB交于点C.
x2+bx+c经过点A和点F,与直线AB交于点C.
(1)求b和c的值;
(2)点P是直线AC下方的抛物线上的一动点,连结PA,PB.求△PAB的最大面积及点P到直线AC的最大距离;
(3)点Q是抛物线上一点,点D在坐标轴上,在(2)的条件下,是否存在以A,P,D,Q为顶点且AP为边的平行四边形,若存在,直接写出点Q的坐标;若不存在,说明理由.
【答案】(1)b=![]() ,c=﹣
,c=﹣![]() ;(2)
;(2)![]() ,
,![]() ;(3)点Q的坐标为:(﹣1﹣
;(3)点Q的坐标为:(﹣1﹣![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(﹣1+
)或(﹣1+![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
(1)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,则点
,则点![]() 、
、![]() 的坐标分别为:
的坐标分别为:![]() 、
、![]() ,则点
,则点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,则
,则![]() ,将点
,将点![]() 的坐标代入抛物线表达式并解得:
的坐标代入抛物线表达式并解得:![]() ;
;
(2)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设出点P,H的坐标,将△PAB的面积表示成△APH和△BPH的面积之和,可得函数表达式,可求△PAB的面积最大值,此时设点P到AB的距离为d,当△PAB的面积最大值时d最大,利用面积公式求出d.
,设出点P,H的坐标,将△PAB的面积表示成△APH和△BPH的面积之和,可得函数表达式,可求△PAB的面积最大值,此时设点P到AB的距离为d,当△PAB的面积最大值时d最大,利用面积公式求出d.
(3)若存在以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点且
为顶点且![]() 为边的平行四边形时,平移AP,得出所有可能的情形,利用平行四边形的对称性得到坐标的关系,即可求解.
为边的平行四边形时,平移AP,得出所有可能的情形,利用平行四边形的对称性得到坐标的关系,即可求解.
解:(1)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
令x=0,则y=![]() ,令y=0,则x=-3,
,令y=0,则x=-3,
则点![]() 、
、![]() 的坐标分别为:
的坐标分别为:![]() 、
、![]() ,
,
∵点F是点B关于x轴的对称点,
∴点![]() ,
,
∵抛物线![]() 经过点
经过点![]() 和点
和点![]() ,则
,则![]() ,
,
将点![]()
![]() 代入抛物线表达式得:
代入抛物线表达式得:![]() ,
,
解得:![]() ,
,
故抛物线的表达式为:![]() ,
,
![]() ,
,![]() ;
;
(2)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,
,
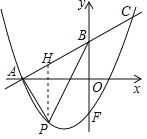
设点![]() ,则点
,则点![]() ,
,
则![]() 的面积:
的面积:
![]()
![]()
当![]() 时,
时,
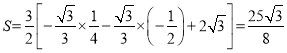 ,
,
且![]() ,
,
∴![]() 的最大值为
的最大值为![]() ,此时点
,此时点![]() ,
,![]() ,
,
设:![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() ,
,![]()
![]() ,解得:
,解得:![]() ;
;
(3)存在,理由:
点![]() ,点
,点![]() ,
,![]() ,设点
,设点![]() ,
,![]() ,
,
①当点![]() 在
在![]() 轴上时,
轴上时,
若存在以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点且
为顶点且![]() 为边的平行四边形时,如图,
为边的平行四边形时,如图,
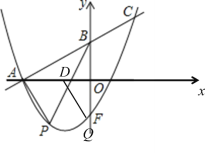
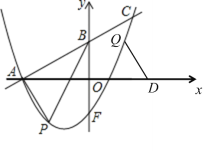
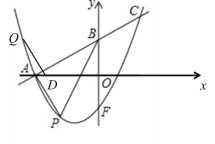
三种情形都可以构成平行四边形,
由于平行四边形的对称性可得图中点Q到x轴的距离和点P到x轴的距离相等,
∴![]() ,
,
即![]() ,
,
解得:![]() (舍去)或
(舍去)或![]() 或
或![]() ;
;
②当点![]() 在
在![]() 轴上时,如图:
轴上时,如图:
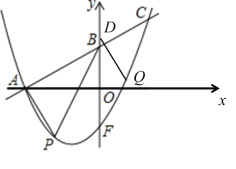
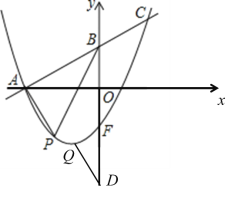
当点Q在y轴右侧时,由平行四边形的性质可得:
![]() =3,
=3,
∴![]()
∴m=![]() ,代入二次函数表达式得:y=
,代入二次函数表达式得:y=![]()
当点Q在y轴左侧时,由平行四边形的性质可得:
![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,代入二次函数表达式得:y=
,代入二次函数表达式得:y=![]()
故点![]() ,
,![]() 或
或![]() ,
,![]() ;
;
故点![]() 的坐标为:
的坐标为:![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() .
.

 阅读快车系列答案
阅读快车系列答案