题目内容
一个反比例函数的图象经过点A(1,3),O是原点,
(1)求该反比例函数解析式;
(2)点B是反比例函数图象上一点,过点B做BC⊥x轴于C,做BD⊥y轴于D,四边形OCBD的周长为8,求OB长.
(1)求该反比例函数解析式;
(2)点B是反比例函数图象上一点,过点B做BC⊥x轴于C,做BD⊥y轴于D,四边形OCBD的周长为8,求OB长.
分析:(1)设反比例函数解析式为y=
,将点A(1,3)代入y=
即可得到k=3,从而得到函数解析式;
(2)根据反比例函数k的几何意义求出四边形的面积,再结合四边形的周长求出OC2+BC2的值,根据勾股定理即可得到OB的长.
| k |
| x |
| k |
| x |
(2)根据反比例函数k的几何意义求出四边形的面积,再结合四边形的周长求出OC2+BC2的值,根据勾股定理即可得到OB的长.
解答: 解:(1)设反比例函数解析式为y=
解:(1)设反比例函数解析式为y=
,
将点A(1,3)代入y=
得,k=3,
则函数解析式为y=
.
(2)∵四边形OCBD为矩形,
∴四边形OCBD的面积为3,
∴OC•CB=3,
∵OC+BC=4,
∴(OC+BC)2=16,
∴OC2+BC2+2OC•BC=16,
∴OC2+BC2=16-2OC•BC,
∴OB2=16-2×3=10;
∴OB=
.
 解:(1)设反比例函数解析式为y=
解:(1)设反比例函数解析式为y=| k |
| x |
将点A(1,3)代入y=
| k |
| x |
则函数解析式为y=
| 3 |
| x |
(2)∵四边形OCBD为矩形,
∴四边形OCBD的面积为3,
∴OC•CB=3,
∵OC+BC=4,
∴(OC+BC)2=16,
∴OC2+BC2+2OC•BC=16,
∴OC2+BC2=16-2OC•BC,
∴OB2=16-2×3=10;
∴OB=
| 10 |
点评:本题考查了反比函数的几何意义以及待定系数法求函数解析式,要灵活运用所学知识进行解答.

练习册系列答案
相关题目
 3+3
3+3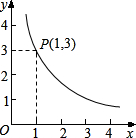 如图所示的曲线是一个反比例函数的图象的一支,且经过点P(1,3)
如图所示的曲线是一个反比例函数的图象的一支,且经过点P(1,3)