题目内容
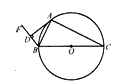
 已知如图,半径为2的⊙A与直线l相切于C,点B与⊙A在l的同旁,与l的距离BD=6,DC=15,点P为l上到A、B两点距离之和为最短的一点,试确定P点的位置,并求出PC和PD.
已知如图,半径为2的⊙A与直线l相切于C,点B与⊙A在l的同旁,与l的距离BD=6,DC=15,点P为l上到A、B两点距离之和为最短的一点,试确定P点的位置,并求出PC和PD.分析:由已知先以l为对称轴作点A的对称点A’,连接BA’,交l与点P,根据轴对称性质及两点之间线段最短确定点P,再根据求两个直角三角形的正切值求出PC和PD.
解答: 解:∵半径为2的⊙A与直线l相切于C,
解:∵半径为2的⊙A与直线l相切于C,
∴以l为对称轴作点A的对称点A′,
连接BA’,交l与点P,
点P即要求的点,
∵PA=PA′,
∴PA+PB=PA′+PB=BA′(两点之间线段最短);
由作图得∠APC=∠A′PC,
∵∠A′PC=∠BPD(对顶角相等),
∴∠BPD=∠APC,
∴由已知在Rt△PDB和Rt△PCA中,
∴tan∠BPD=tan∠APC,
∴
=
,
即
=
,
得:PD=
,
则PC=15-PD=
.
 解:∵半径为2的⊙A与直线l相切于C,
解:∵半径为2的⊙A与直线l相切于C,∴以l为对称轴作点A的对称点A′,
连接BA’,交l与点P,
点P即要求的点,
∵PA=PA′,
∴PA+PB=PA′+PB=BA′(两点之间线段最短);
由作图得∠APC=∠A′PC,
∵∠A′PC=∠BPD(对顶角相等),
∴∠BPD=∠APC,
∴由已知在Rt△PDB和Rt△PCA中,
∴tan∠BPD=tan∠APC,
∴
| BD |
| PD |
| AC |
| DC-PD |
即
| 6 |
| PD |
| 2 |
| 15-PD |
得:PD=
| 45 |
| 4 |
则PC=15-PD=
| 15 |
| 4 |
点评:此题考查的知识点是切线的性质,关键是运用轴对称,两点之间线段最短及三角函数值解答.

练习册系列答案
相关题目
 如图,半径为r1的圆内切于半径为r2的圆,切点为P,弦AB经过O1交⊙O1于C,D.已知AC:CD:DB=3:4:2,则
如图,半径为r1的圆内切于半径为r2的圆,切点为P,弦AB经过O1交⊙O1于C,D.已知AC:CD:DB=3:4:2,则
 已知如图,半径为2的⊙A与直线l相切于C,点B与⊙A在l的同旁,与l的距离BD=6,DC=15,点P为l上到A、B两点距离之和为最短的一点,试确定P点的位置,并求出PC和PD.
已知如图,半径为2的⊙A与直线l相切于C,点B与⊙A在l的同旁,与l的距离BD=6,DC=15,点P为l上到A、B两点距离之和为最短的一点,试确定P点的位置,并求出PC和PD.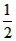 ,求⊙O的半径。
,求⊙O的半径。