题目内容
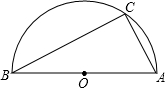
已知如图,⊙O为△ABC的外接圆,BC为⊙O的直径,作射线BF,使得BA平分∠CBF,过点A作AD⊥ BF于点D。
(1)求证:DA为⊙O的切线;
(2)若BD=1,tan∠BAD=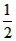 ,求⊙O的半径。
,求⊙O的半径。
(1)求证:DA为⊙O的切线;
(2)若BD=1,tan∠BAD=
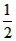 ,求⊙O的半径。
,求⊙O的半径。 
|
解:(1)连接AO, |
 |
| (2)∵AD⊥DB,BD=1,tan∠BAD=1/2, ∴AD=2, 由勾股定理,得  ∴sin ∠4=  ∵BC是⊙O直径, ∴∠BAC=90°, ∴∠C+∠2=90°, 又∵∠4+∠1=90°,∠2=∠1, ∴∠4=∠C, 在Rt △ABC中, BC=  = = =5, =5,∴⊙O的半径为5/2。 |

练习册系列答案
相关题目
 21、已知如图,AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD.求证:AD是⊙O的切线.
21、已知如图,AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD.求证:AD是⊙O的切线.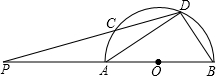 已知如图,AB为半圆的直径,C、D为半圆弧上的两点,若弧CD=弧BD,DC与BA的延长线交于P,如果,AP:CP=3:4,△ADB的面积为
已知如图,AB为半圆的直径,C、D为半圆弧上的两点,若弧CD=弧BD,DC与BA的延长线交于P,如果,AP:CP=3:4,△ADB的面积为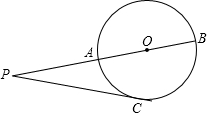 已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P,O两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=
已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P,O两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=