题目内容
【题目】如图，
是
的弦，
为半径
的中点，过作
交弦于点
，交于点
，且
是的切线.
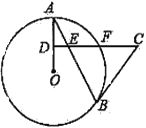
(1)求证：
；
(2)连接
，
，求
；
(3)如果
，
，
，求的半径.
【答案】(1)证明见解析；(2)
；(3)
的半径为
．
【解析】
(1)连接OB，根据切线的性质得到
根据等角的余角相等得到
对顶角相等得到
，等量代换得到
即可证明.
(2)连接OF，AF，BF，首先证明△OAF是等边三角形，再利用圆周角定理：同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数,即可求解.
(3)过点
作
于点
,根据等腰三角形的性质得到
，在
中,
设
,
,则
，证明
，根据相似三角形的性质得到
即
，解得
，求出
，即可求出的半径为．
(1)证明：如图，连接OB
∵
∴
∵
切⊙O于
∴
∴
∴
∵
∴
∴
∴
∴
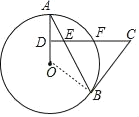
(2)解：连接
,
,
∵
,
∴
∵
∴
∴
是等边三角形
∴
∴
∴
(3)过点作于点
∵
∴
∵在中,
设,,则
∵,
∴
又∵
∴
∴ 即
∴
∴
∴
即的半径为．
练习册系列答案
53随堂测系列答案
相关题目
