Question

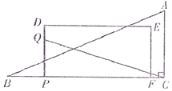
【题目】如图，AB、CD为两个建筑物，建筑物AB的高度为100米，从建筑物AB的顶点A处测得建筑物CD的顶部C处的俯角∠EAC为30°，测得建筑物CD的底部D处的俯角∠EAD为45°．

（1）求两建筑物底部之间水平距离BD的长度；

（2）求建筑物CD的高度（结果保留根号）．

Answer 1

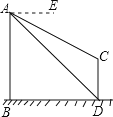
【答案】（1）两建筑物底部之间水平距离BD的长度为100米；（2）建筑物CD的高度为（100-）米．

【解析】

（1）根据题意得：BD∥AE，从而得到∠BAD=∠ADB=45°，利用BD=AB=100，求得两建筑物底部之间水平距离BD的长度为100米；

（2）延长AE、DC交于点F，根据题意得四边形ABDF为正方形，根据AF=BD=DF=100，在Rt△AFC中利用∠FAC=30°求得CF，然后即可求得CD的长．

解：（1）根据题意得：BD∥AE，

∴∠ADB=∠EAD=45°，

∵∠ABD=90°，

∴∠BAD=∠ADB=45°，

∴BD=AB=100米，

答：两建筑物底部之间水平距离BD的长度为100米；

（2）延长AE、DC交于点F，根据题意得四边形ABDF为正方形，

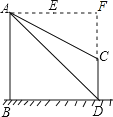
∴AF=BD=DF=100米，

在Rt△AFC中，∠FAC=30°，

∴CF=AFtan∠FAC=100×=米，

又∵FD=100米，

∴CD=10-（米）．

答：建筑物CD的高度为（100-）米．