题目内容
已知a、b都是常数，一次函数y=（m-2）x+（m+3）经过点（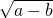
，
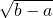），则这个一次函数的解析式为________．
y=-5x
分析：根据非负数的性质列式求出a=b，从而得到经过的点的坐标为（0，0），再把点的坐标代入函数解析式求出m的值，即可得解．
解答：根据非负数的性质得，a-b≥0且b-a≥0，
解得a≥b且b≥a，
所以，a=b，
所以，点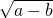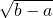（，）为（0，0），
代入一次函数y=（m-2）x+（m+3）得，m+3=0，
解得m=-3，
所以，m-2=-3-2=-5，
因此，这个一次函数的解析式为y=-5x．
故答案为：y=-5x．
点评：本题考查了一次函数图象上点的坐标特征，根据非负数的性质求出a=b，从而得到经过的点的坐标是（0，0）是解题的关键．
分析：根据非负数的性质列式求出a=b，从而得到经过的点的坐标为（0，0），再把点的坐标代入函数解析式求出m的值，即可得解．
解答：根据非负数的性质得，a-b≥0且b-a≥0，
解得a≥b且b≥a，
所以，a=b，
所以，点（
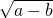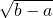，）为（0，0），代入一次函数y=（m-2）x+（m+3）得，m+3=0，
解得m=-3，
所以，m-2=-3-2=-5，
因此，这个一次函数的解析式为y=-5x．
故答案为：y=-5x．
点评：本题考查了一次函数图象上点的坐标特征，根据非负数的性质求出a=b，从而得到经过的点的坐标是（0，0）是解题的关键．
练习册系列答案
相关题目
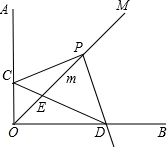（2013•宝山区一模）已知∠AOB=90°，OM是∠AOB的平分线，将一个直角三角板的直角顶点P放在射线OM上，OP=m（m为常数且m≠0），移动直角三角板，两边分别交射线OA，OB与点C，D