题目内容
解方程：（x2-x）2-2（x2-x）-3=0
解：设x2-x=y，所以原方程变化为：y2-2y-3=0，
解得y=-1或3，
当y=-1时，x2-x=-1，无解；
当y=3时，x2-x=3，
解得，x1=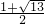
，x2=
，
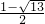∴原方程的解为x1=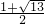，x2=．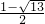
分析：把原方程中的（x2-x）代换成y，即可得到关于y的方程．
点评：本题主要考查换元法在解一元二次方程中的应用．换元法是借助引进辅助元素，将问题进行转化的一种解题方法．这种方法在解题过程中，把某个式子看作一个整体，用一个字母去代表它，实行等量替换．这样做，常能使问题化繁为简，化难为易，形象直观．
解得y=-1或3，
当y=-1时，x2-x=-1，无解；
当y=3时，x2-x=3，
解得，x1=
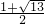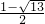，x2=，∴原方程的解为x1=
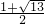，x2=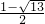．分析：把原方程中的（x2-x）代换成y，即可得到关于y的方程．
点评：本题主要考查换元法在解一元二次方程中的应用．换元法是借助引进辅助元素，将问题进行转化的一种解题方法．这种方法在解题过程中，把某个式子看作一个整体，用一个字母去代表它，实行等量替换．这样做，常能使问题化繁为简，化难为易，形象直观．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
用换元法解方程
+
=
，若设
=y．则原方程可化为（ ）
| 3x |
| x2-1 |
| x2-1 |
| x |
| 5 |
| 2 |
| x |
| x2-1 |
A、y+
| ||||
| B、2y2-5y+2=0 | ||||
C、3y+
| ||||
| D、6y2+5y+2=0 |