题目内容
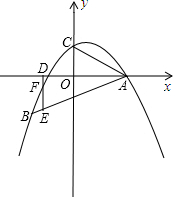
如图,二次函数y=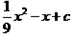 的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).
的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).
(1)求m、n的值.
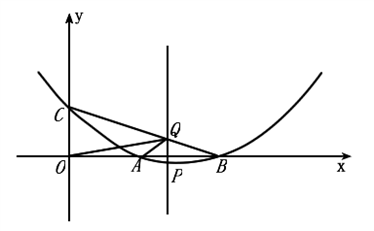
(2)设P(x, y)(0< x < n)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①线段PQ的长度是否存在最大值?如果存在,最大值是多少?如果不存在,请说明理由
②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由。
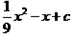 的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).
的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).(1)求m、n的值.
(2)设P(x, y)(0< x < n)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①线段PQ的长度是否存在最大值?如果存在,最大值是多少?如果不存在,请说明理由
②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由。
解:(1) ∵抛物线过C(0 ,2) ,∴OC=2.
∵抛物线过A(m,0)、B(n,0),
∴m、n是一元二次方程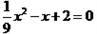 的两根, 解得
的两根, 解得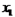 =3,
=3, 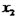 =6.
=6.
∴m=3,n=6.
(2)①存在.
设直线BC的函数解析式为y=kx+b.
则有 解得
解得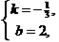
∴直线BC的函数解析式为y=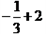 . ∵ 0< x <6.
. ∵ 0< x <6.
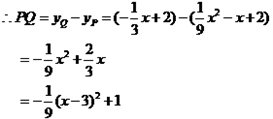
∴当x=3时,线段PQ的长度取得最大值,最大值为1
②存在这样的点P,使△OAQ为直角三角形. 分以下三种情况进行讨论来求点P的坐标:
当∠OAQ =90°时,点P与点A重合,
∴ (3,0).当∠QOA =90°时,点P与点C重合,
(3,0).当∠QOA =90°时,点P与点C重合,
∴x =0(不合题意)
当∠OQA =90°时,设Po与x轴交于点D,如图.
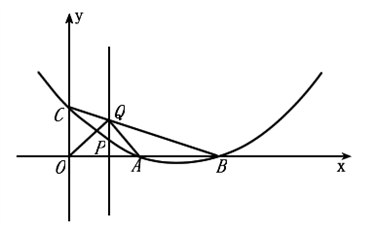
∵ ∠QOD + ∠OQD =90°,∠OQD+ ∠AQD=90°,
∴∠QOD= ∠AQD.
又∵ ∠ODQ= ∠QDA =90°
∴△ODQ∽△QDA,
∴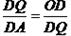 ,即
,即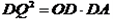
∴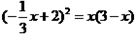 . 整理得
. 整理得 =0,解得
=0,解得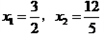 .
.
∴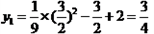 ,
,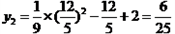
∴ .
.
综上,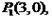
 .
.
∵抛物线过A(m,0)、B(n,0),
∴m、n是一元二次方程
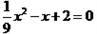 的两根, 解得
的两根, 解得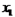 =3,
=3, 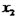 =6.
=6. ∴m=3,n=6.
(2)①存在.
设直线BC的函数解析式为y=kx+b.
则有
 解得
解得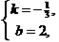
∴直线BC的函数解析式为y=
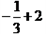 . ∵ 0< x <6.
. ∵ 0< x <6.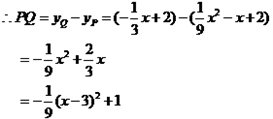
∴当x=3时,线段PQ的长度取得最大值,最大值为1
②存在这样的点P,使△OAQ为直角三角形. 分以下三种情况进行讨论来求点P的坐标:
当∠OAQ =90°时,点P与点A重合,
∴
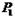 (3,0).当∠QOA =90°时,点P与点C重合,
(3,0).当∠QOA =90°时,点P与点C重合,∴x =0(不合题意)
当∠OQA =90°时,设Po与x轴交于点D,如图.

∵ ∠QOD + ∠OQD =90°,∠OQD+ ∠AQD=90°,
∴∠QOD= ∠AQD.
又∵ ∠ODQ= ∠QDA =90°
∴△ODQ∽△QDA,
∴
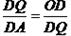 ,即
,即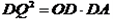
∴
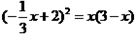 . 整理得
. 整理得 =0,解得
=0,解得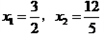 .
. ∴
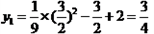 ,
,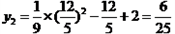
∴
 .
.综上,
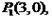
 .
. 
练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 如图,二次函数y=
如图,二次函数y=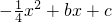 的图象过点A(4,0),B(-4,-4),与y轴交于点C.
的图象过点A(4,0),B(-4,-4),与y轴交于点C.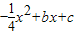 的图象过点A(4,0),B(-4,-4),与y轴交于点C.
的图象过点A(4,0),B(-4,-4),与y轴交于点C.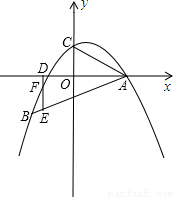
 图像的一部分,该图在
图像的一部分,该图在 轴右侧与
轴右侧与 轴交点的坐标是
轴交点的坐标是

 图像的一部分,该图在
图像的一部分,该图在 轴右侧与
轴右侧与 轴交点的坐标是
轴交点的坐标是 