题目内容
如图,二次函数y=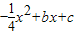 的图象过点A(4,0),B(-4,-4),与y轴交于点C.
的图象过点A(4,0),B(-4,-4),与y轴交于点C.(1)证明:∠BAO=∠CAO(其中O是原点);
(2)在抛物线的对称轴上求一点P,使|CP+BP|的值最小;
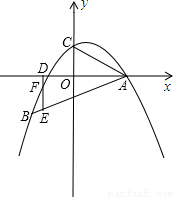
(3)若E是线段AB上的一个动点(不与A、B重合),过E作y轴的平行线,分别交此二次函数图象及x轴于F、D两点.请问是否存在这样的点E,使DE=2DF?若存在,请求出点E的坐标;若不存在,说明理由.
【答案】分析:(1)首先利用待定系数法求出二次函数解析式,进而得出C点坐标,得出tan∠BAO=tan∠CAO即可得出答案;
(2)根据C点关于对称轴直线x=1对称的点为C′(2,2),P点为BC′与x=1的交点,此时|CP+BP|的值最小,得出P的坐标即可;
(3)根据图象得出DE,DF的长,进而分别求出x的值即可.
解答: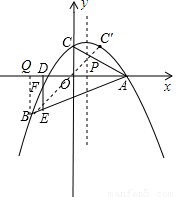 (1)证明:过点B作BQ⊥x轴于点D,
(1)证明:过点B作BQ⊥x轴于点D,
∵二次函数y=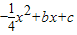 的图象过点A(4,0),B(-4,-4),
的图象过点A(4,0),B(-4,-4),
∴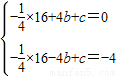 ,
,
解得: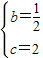
∴抛物线解析式为y=- x2+
x2+ x+2,
x+2,
∴C点坐标为:(0,2),
∴CO=2,AO=4,BQ=4,AQ=4+4=8,
∵tan∠BAO=tan∠CAO=0.5,
∴∠BAO=∠CAO;
(2)解:∵C点关于对称轴直线x=1对称的点为C′(2,2),P点为BC′与x=1的交点,
∴P的坐标为(1,1),
此时|CP+BP|的值最小;
(3)解:AB:y= x-2,设E(x,
x-2,设E(x, x-2),(-4<x<4),
x-2),(-4<x<4),
则F(x,- x2+
x2+ x+2),DE=|
x+2),DE=| x-2|=2-
x-2|=2- x,DF=|-
x,DF=|- x2+
x2+ x+2|
x+2|
当2- x=
x= x2+x+4,
x2+x+4,
解得:x1=-1,x2=4(舍去),所以E(-1,- ),
),
当2- x=-
x=- x2-x-4,
x2-x-4,
解得:x1=-3,x2=4(舍去),所以E(-3,- ).
).
综上所述:点E的坐标为:(-1,- ),(-3,-
),(-3,- ).
).
点评:此题主要考查了二次函数的综合应用以及轴对称求最小值问题和点的坐标性质,注意利用绝对值的性质得出是解题关键.
(2)根据C点关于对称轴直线x=1对称的点为C′(2,2),P点为BC′与x=1的交点,此时|CP+BP|的值最小,得出P的坐标即可;
(3)根据图象得出DE,DF的长,进而分别求出x的值即可.
解答:
 (1)证明:过点B作BQ⊥x轴于点D,
(1)证明:过点B作BQ⊥x轴于点D,∵二次函数y=
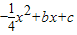 的图象过点A(4,0),B(-4,-4),
的图象过点A(4,0),B(-4,-4),∴
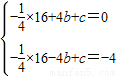 ,
,解得:
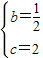
∴抛物线解析式为y=-
 x2+
x2+ x+2,
x+2,∴C点坐标为:(0,2),
∴CO=2,AO=4,BQ=4,AQ=4+4=8,
∵tan∠BAO=tan∠CAO=0.5,
∴∠BAO=∠CAO;
(2)解:∵C点关于对称轴直线x=1对称的点为C′(2,2),P点为BC′与x=1的交点,
∴P的坐标为(1,1),
此时|CP+BP|的值最小;
(3)解:AB:y=
 x-2,设E(x,
x-2,设E(x, x-2),(-4<x<4),
x-2),(-4<x<4),则F(x,-
 x2+
x2+ x+2),DE=|
x+2),DE=| x-2|=2-
x-2|=2- x,DF=|-
x,DF=|- x2+
x2+ x+2|
x+2|当2-
 x=
x= x2+x+4,
x2+x+4,解得:x1=-1,x2=4(舍去),所以E(-1,-
 ),
),当2-
 x=-
x=- x2-x-4,
x2-x-4,解得:x1=-3,x2=4(舍去),所以E(-3,-
 ).
).综上所述:点E的坐标为:(-1,-
 ),(-3,-
),(-3,- ).
).点评:此题主要考查了二次函数的综合应用以及轴对称求最小值问题和点的坐标性质,注意利用绝对值的性质得出是解题关键.

练习册系列答案
相关题目
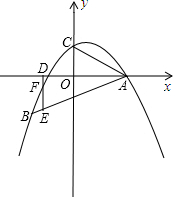 如图,二次函数y=
如图,二次函数y=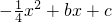 的图象过点A(4,0),B(-4,-4),与y轴交于点C.
的图象过点A(4,0),B(-4,-4),与y轴交于点C.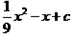 的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).
的图象与x轴的交点是A(m,0)、B(n,0),与y轴的交点是C(0, 2).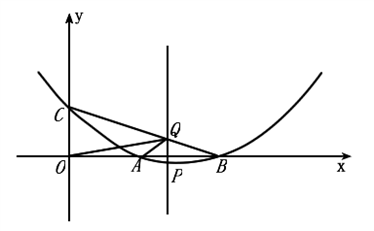
 图像的一部分,该图在
图像的一部分,该图在 轴右侧与
轴右侧与 轴交点的坐标是
轴交点的坐标是

 图像的一部分,该图在
图像的一部分,该图在 轴右侧与
轴右侧与 轴交点的坐标是
轴交点的坐标是 