题目内容
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: ≈1.41,
≈1.41, ≈1.73).
≈1.73).

解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH= ,
,
∴CH=AH•tan∠CAH,
∴CH=AH•tan∠CAH=6tan30°=6× (米),
(米),
∵DH=1.5,∴CD=2 +1.5,
+1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED= ,
,
∴CE= =4+
=4+ ≈5.7(米),
≈5.7(米),
答:拉线CE的长约为5.7米.


练习册系列答案
相关题目
平行四边形的内角和为( )
|
| A. | 180° | B. | 270° | C. | 360° | D. | 640° |
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )

|
| A. | 30 | B. | 45 | C. | 60 | D. | 90 |
2014年4月25日青岛世界园艺博览会成功开幕,预计将接待1500万人前来观赏,将1500万用科学记数法表示为( )
|
| A. | 15×105 | B. | 1.5×106 | C. | 1.5×107 | D. | 0.15×108 |
 的解集是( )
的解集是( )
 取1.73,结果精确到0.1m)
取1.73,结果精确到0.1m)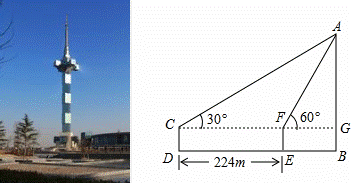


 .
.