题目内容
8.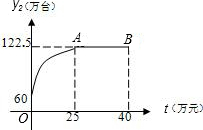 某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=$\left\{\begin{array}{l}{3x(0≤x≤25)}\\{2x+25(25≤x≤40)}\end{array}\right.$.该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示.其中点A为抛物线的顶点.
某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足y1=$\left\{\begin{array}{l}{3x(0≤x≤25)}\\{2x+25(25≤x≤40)}\end{array}\right.$.该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示.其中点A为抛物线的顶点.(1)结合图象,求出y2(万台)与外地广告费用t(万元)之间的函数关系式;
(2)求该产品的销售总量y(万台)与本地广告费用x(万元)之间的函数关系式(其中y=y1+y2);
(3)若本地的广告费用不低于25万元,则销售总量最大的是多少?
分析 (1)当0≤t≤25时,y2为二次函数,顶点坐标为(25,122.5),设抛物线顶点式,把(0,60)代入求函数式,当25<t≤40时,y2=122.5;
(2)由x+t=40,得t=40-x,此时,x的取值范围是0≤x<15,15≤x<25,25≤x≤40,由y=y1+y2,分别求该产品的销售总量y(万台)与本地广告费用x(万元)之间的函数关系式;
(3)由(2)中的两个函数关系式,再各范围内求y的最大值,比较即可.
解答 解:(1)当0≤t≤25时,抛物线顶点坐标为(25,122.5),设y2=a(t-25)2+122.5,
将(0,60)代入,得a(0-25)2+122.5=60,
解得a=-$\frac{1}{10}$,
y2=-$\frac{1}{10}$(t-25)2+122.5,
当25<t≤40时,y2=122.5;
(2)由x+t=40,根据t的取值范围得,
当0≤x<15时,y=y1+y2=3x+122.5,
当15≤x<25时,y=y1+y2=3x-$\frac{1}{10}$(40-x-25)2+122.5=-0.1x2+3x+100;
当25≤x≤40时,y=y1+y2=2x+25+122.5=2x+147.5;
(3)由(2)的函数关系式可知,当x=40时,y最大=227.5万元,
即:安排本地广告费40万元,外地广告费10万元,能使销售总量最大,最大为227.5万元.
点评 本题考查了二次函数的应用.关键是根据函数图象,分段求出y2的函数关系式及t的取值范围,根据两个变量x、t的和为40,将函数式中的变量进行转化,根据二次函数的性质求最大值.

练习册系列答案
相关题目
20.下列四个图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.下列各组两项属于同类项的是( )
| A. | 3x2y与8y2x | B. | 2m和2n | C. | 6与-8 | D. | x3和43 |