题目内容
4. 如图,四边形ABCD内接于⊙O,E为BC延长线上一点,∠A=50°,则∠DCE的度数为( )
如图,四边形ABCD内接于⊙O,E为BC延长线上一点,∠A=50°,则∠DCE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 130° |
分析 连接OB,OD,利用圆周角定理得到∠DOB=2∠A,∠DOB(大于平角的角)=2∠BCD,再由周角定义及等式的性质得到∠A与∠BCD互补,利用邻补角性质及同角的补角相等即可求出所求角的度数.
解答  解:连接OB,OD,
解:连接OB,OD,
∵∠DOB与∠A都对$\widehat{BD}$,∠DOB(大于平角的角)与∠BCD都对$\widehat{DAB}$,
∴∠DOB=2∠A,∠DOB(大于平角的角)=2∠BCD,
∵∠DOB+∠DOB(大于平角的角)=360°,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠DCE=∠A=50°,
故选B
点评 此题考查了圆内接四边形的性质,以及圆周角定理,熟练掌握圆周角定理是解本题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
10.对部分参加夏令营的中学生的年龄(单位:岁)进行统计,结果如表:
则这些学生年龄的众数是17岁.
| 年龄 | 13 | 14 | 15 | 16 | 17 | 18 |
| 人数 | 4 | 5 | 6 | 6 | 7 | 2 |
19.非零数a的倒数是( )
| A. | a | B. | |a| | C. | $\frac{1}{a}$ | D. | -a |
9. 如图,AB是⊙O的直径,点C、D是⊙O上的两点,若BC∥DO,∠D=35°,则∠A的度数是( )
如图,AB是⊙O的直径,点C、D是⊙O上的两点,若BC∥DO,∠D=35°,则∠A的度数是( )
 如图,AB是⊙O的直径,点C、D是⊙O上的两点,若BC∥DO,∠D=35°,则∠A的度数是( )
如图,AB是⊙O的直径,点C、D是⊙O上的两点,若BC∥DO,∠D=35°,则∠A的度数是( )| A. | 20° | B. | 15° | C. | 10° | D. | 25° |
13.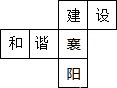 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面的字是( )
一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面的字是( )
 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面的字是( )
一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面的字是( )| A. | 和 | B. | 谐 | C. | 襄 | D. | 阳 |
14.实数a,b互为相反数,则下列结论正确的是( )
| A. | a+b=0 | B. | ab=1 | C. | a÷b=-l | D. | a>0,b<0 |
 如图,小明在窗台C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知窗台C处离地面的距离CD为5m,则大树的高度为5+5$\sqrt{3}$m.(结果保留根号)
如图,小明在窗台C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知窗台C处离地面的距离CD为5m,则大树的高度为5+5$\sqrt{3}$m.(结果保留根号)