题目内容
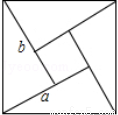
如图，我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形与大正方形的面积之比为1：13，则直角三角形较短的直角边a与较长的直角边b的比值为 ．
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
如图，我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形与大正方形的面积之比为1：13，则直角三角形较短的直角边a与较长的直角边b的比值为 ．
阅读快车系列答案
与双曲线
的交点A的横坐标1，则关于x的不等式
的解集是（ ）
，令
，可得
，我们就说1是函数
的零点．
（
为常数）．
时，求该函数的零点；
取何值，该函数总有两个零点．
相交于A、B两点，A点的坐标为（1，2）
x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知B点的坐标为B（8，0）．