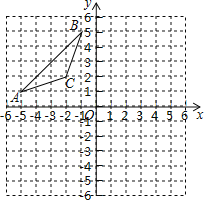ĢāÄæÄŚČŻ
”¾ĢāÄæ”æijŠ£ĪŖÅąÓżĒąÉŁÄźæĘ¼¼““ŠĀÄÜĮ¦£¬¾Ł°ģĮĖ¶ÆĀžÖĘ×÷»ī¶Æ£¬Š”Ć÷Éč¼ĘĮĖµć×öŌ²ÖÜŌĖ¶ÆµÄŅ»øö³ūŠĪ£¬ČēĶ¼ĖłŹ¾£¬¼×”¢ŅŅĮ½µć·Ö±š“ÓÖ±¾¶µÄĮ½¶Ėµć![]() ”¢
”¢![]() £¬ŅŌĖ³Ź±Õė”¢ÄꏱÕėµÄ·½ĻņĶ¬Ź±ŃŲŌ²ÖÜŌĖ¶Æ£¬¼×ŌĖ¶ÆµÄĀ·³Ģ
£¬ŅŌĖ³Ź±Õė”¢ÄꏱÕėµÄ·½ĻņĶ¬Ź±ŃŲŌ²ÖÜŌĖ¶Æ£¬¼×ŌĖ¶ÆµÄĀ·³Ģ![]() ÓėŹ±¼ä
ÓėŹ±¼ä![]() Āś×ć¹ŲĻµ
Āś×ć¹ŲĻµ![]() £¬ŅŅŅŌ
£¬ŅŅŅŌ![]() µÄĖŁ¶ČŌČĖŁŌĖ¶Æ£¬°ėŌ²µÄ³¤¶ČĪŖ
µÄĖŁ¶ČŌČĖŁŌĖ¶Æ£¬°ėŌ²µÄ³¤¶ČĪŖ![]() £®
£®
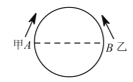
£Ø1£©¼×ŌĖ¶Æ![]() ŗóµÄĀ·³ĢŹĒ¶ąÉŁ?
ŗóµÄĀ·³ĢŹĒ¶ąÉŁ?
£Ø2£©¼×”¢ŅŅ“ÓæŖŹ¼ŌĖ¶Æµ½µŚŅ»“ĪĻąÓöŹ±£¬ĖüĆĒŌĖ¶ÆĮĖ¶ąÉŁŹ±¼ä?
£Ø3£©¼×”¢ŅŅ“ÓæŖŹ¼ŌĖ¶Æµ½µŚ¶ž“ĪĻąÓöŹ±£¬ĖüĆĒŌĖ¶ÆĮĖ¶ąÉŁŹ±¼ä?
”¾“š°ø”æ£Ø1£©28cm£»£Ø2£©3s£»£Ø3£©7s
”¾½āĪö”æ
£Ø1£©½«t=4“śČė¹«Ź½¼ĘĖć¼“æÉ£»
£Ø2£©µŚŅ»“ĪĻąÓö¼“ŹĒ¹²×ß°ėŌ²µÄ³¤¶Č£¬¾Ż“ĖĮŠ·½³Ģ![]() £¬Ēó½ā¼“æÉ£»
£¬Ēó½ā¼“æÉ£»
£Ø3£©µŚ¶ž“ĪĻąÓöÓ¦ŹĒ×ßĮĖČżøö°ėŌ²µÄ³¤¶Č£¬µĆµ½![]() £¬½ā·½³Ģ¼“æɵƵ½“š°ø.
£¬½ā·½³Ģ¼“æɵƵ½“š°ø.
½ā£ŗ£Ø1£©µ± t=4s Ź±£¬![]() cm.
cm.
“š£ŗ¼×ŌĖ¶Æ 4s ŗóµÄĀ·³ĢŹĒ ![]() £®
£®
£Ø2£© ÓÉĶ¼æÉÖŖ£¬¼×ŅŅµŚŅ»“ĪĻąÓöŹ±×ß¹żµÄĀ·³ĢĪŖ°ėŌ² ![]() £¬¼××ß¹żµÄĀ·³ĢĪŖ
£¬¼××ß¹żµÄĀ·³ĢĪŖ ![]() £¬
£¬
ŅŅ×ß¹żµÄĀ·³ĢĪŖ ![]() £¬Ōņ
£¬Ōņ![]() .
.
½āµĆ ![]() »ņ
»ņ ![]() £Ø²»ŗĻĢāŅā£¬ÉįČ„£©£®
£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£®
“š£ŗ¼×”¢ŅŅ“ÓæŖŹ¼ŌĖ¶Æµ½µŚŅ»“ĪĻąÓöŹ±£¬ĖüĆĒŌĖ¶ÆĮĖ 3s£®
£Ø3£© ÓÉĶ¼æÉÖŖ£¬¼×ŅŅµŚ¶ž“ĪĻąÓöŹ±×ß¹żµÄĀ·³ĢĪŖČżøö°ėŌ² ![]() £¬
£¬
Ōņ![]()
½āµĆ ![]() »ņ
»ņ ![]() £Ø²»ŗĻĢāŅā£¬ÉįČ„£©£®
£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£®
“š£ŗ¼×”¢ŅŅ“ÓæŖŹ¼ŌĖ¶Æµ½µŚ¶ž“ĪĻąÓöŹ±£¬ĖüĆĒŌĖ¶ÆĮĖ 7s£®

”¾ĢāÄæ”æ¾ÅÄź¼¶£Ø1£©°ąµÄŠ”»ŖŗĶŠ”ŗģĮ½Ćūѧɜ10“ĪŹżŃ§²āŹŌ³É¼ØČēĻĀ±ķ£Ø±ķI£©ĖłŹ¾£ŗ
Š”»Ø | 70 | 80 | 90 | 80 | 70 | 90 | 80 | 100 | 60 | 80 |
Š”ŗģ | 90 | 80 | 100 | 60 | 90 | 80 | 90 | 60 | 60 | 90 |
ĻÖøł¾ŻÉĻ±ķŹż¾Ż½ųŠŠĶ³¼ĘµĆµ½ĻĀ±ķ£Ø±ķ¢ņ£©£ŗ
ŠÕĆū | Ę½¾ł³É¼Ø | ÖŠĪ»Źż | ÖŚŹż |
Š”»Ŗ | 80 | ||
Š”ŗģ | 80 | 90 |
£Ø1£©ĢīæÕ£ŗøł¾Ż±ķIµÄŹż¾ŻĶź³É±ķ¢ņÖŠĖłČ±µÄŹż¾Ż£»
£Ø2£©ĄĻŹ¦¼ĘĖćĮĖŠ”ŗģµÄ·½²ī![]() ĒėÄć¼ĘĖ抔»ŖµÄ·½²ī²¢ĖµĆ÷ÄÄĆūѧɜµÄ³É¼Ø½ĻĪŖĪČ¶Ø£®
ĒėÄć¼ĘĖ抔»ŖµÄ·½²ī²¢ĖµĆ÷ÄÄĆūѧɜµÄ³É¼Ø½ĻĪŖĪČ¶Ø£®
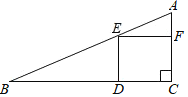
”¾ĢāÄæ”æČēĶ¼1£¬![]() µÄÖ±¾¶
µÄÖ±¾¶![]() £¬µć
£¬µć![]() ĪŖĻ߶Ī
ĪŖĻ߶Ī![]() ÉĻŅ»¶Æµć£¬¹żµć
ÉĻŅ»¶Æµć£¬¹żµć![]() ×÷
×÷![]() µÄ“¹Ļß½»
µÄ“¹Ļß½»![]() ÓŚµć
ÓŚµć![]() £¬
£¬![]() £¬Į¬½į
£¬Į¬½į![]() £¬
£¬![]() .Éč
.Éč![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() £¬
£¬![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() .
.

Š”¶«øł¾ŻŃ§Ļ°ŗÆŹżµÄ¾Ń飬¶ŌŗÆŹż![]() Ėę×Ō±äĮæ
Ėę×Ō±äĮæ![]() µÄ±ä»Æ¶ų±ä»ÆµÄ¹ęĀɽųŠŠĮĖĢ½¾æ.
µÄ±ä»Æ¶ų±ä»ÆµÄ¹ęĀɽųŠŠĮĖĢ½¾æ.
ĻĀĆęŹĒŠ”¶«µÄĢ½¾æ¹ż³Ģ£¬Ēė°ļÖśŠ”¶«Ķź³ÉĻĀĆęµÄĪŹĢā.
£Ø1£©Ķعż¶ŌĶ¼1µÄŃŠ¾æ”¢·ÖĪöÓė¼ĘĖć£¬µĆµ½ĮĖ![]() Óė
Óė![]() µÄ¼ø×é¶ŌÓ¦Öµ£¬ČēĻĀ±ķ£ŗ
µÄ¼ø×é¶ŌÓ¦Öµ£¬ČēĻĀ±ķ£ŗ
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
ĒėĒó³ö±ķÖŠŠ”¶«Ā©ĢīµÄŹż![]() £»
£»
£Ø2£©ČēĶ¼2£¬½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ![]() £¬Ćč³ö±ķÖŠø÷¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£¬»³öøĆŗÆŹżµÄ“óÖĀĶ¼Ļó£»
£¬Ćč³ö±ķÖŠø÷¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£¬»³öøĆŗÆŹżµÄ“óÖĀĶ¼Ļó£»
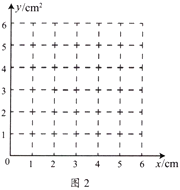
£Ø3£©½įŗĻ»³öµÄŗÆŹżĶ¼Ļ󣬵±![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() Ź±£¬Ēó³ö
Ź±£¬Ēó³ö![]() µÄ³¤.
µÄ³¤.