题目内容
 如图,已知菱形ABCD,边长为10cm,∠ABC=60°,E为对角线BD上一点,且BE=BC,P为CE上一个动点,过P作PN⊥BE于N,PM⊥BC于M,则PM+PN=________.
如图,已知菱形ABCD,边长为10cm,∠ABC=60°,E为对角线BD上一点,且BE=BC,P为CE上一个动点,过P作PN⊥BE于N,PM⊥BC于M,则PM+PN=________.
5
分析:连接BP,作EF⊥BC于点F,有菱形的性质和解直角三角形可求EF,利用面积法得S△BPE+S△BPC=S△BEC,将面积公式代入即可求出PM+PN的值.
解答:连接BP,作EF⊥BC于点F,
则∠EFB=90°,

由菱形的性质可知∠EBF=30°,
∵在直角三角形BEF中,sin∠EBF=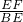 =
= ,BE=BC=10,
,BE=BC=10,
∴EF= BE=5,
BE=5,
又∵PN⊥BD,PM⊥BC,
∴S△BPE+S△BPC=S△BEC,
∴ BE•PN+
BE•PN+ ×BC•PM=
×BC•PM= ×BC×EF,
×BC×EF,
∴PM+PN=EF=5.
故答案为:5.
点评:本题考查了菱形的性质,解决本题的关键是作出辅助线,构造直角三角形,把所求的线段转移到菱形的对角线上.
分析:连接BP,作EF⊥BC于点F,有菱形的性质和解直角三角形可求EF,利用面积法得S△BPE+S△BPC=S△BEC,将面积公式代入即可求出PM+PN的值.
解答:连接BP,作EF⊥BC于点F,
则∠EFB=90°,


由菱形的性质可知∠EBF=30°,
∵在直角三角形BEF中,sin∠EBF=
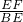 =
= ,BE=BC=10,
,BE=BC=10,∴EF=
 BE=5,
BE=5,又∵PN⊥BD,PM⊥BC,
∴S△BPE+S△BPC=S△BEC,
∴
 BE•PN+
BE•PN+ ×BC•PM=
×BC•PM= ×BC×EF,
×BC×EF,∴PM+PN=EF=5.
故答案为:5.
点评:本题考查了菱形的性质,解决本题的关键是作出辅助线,构造直角三角形,把所求的线段转移到菱形的对角线上.

练习册系列答案
相关题目
 如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
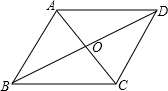 如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
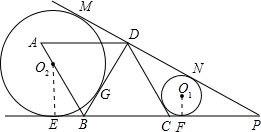 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.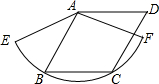 如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的
如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的