题目内容
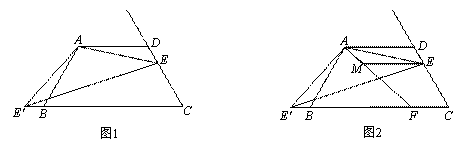
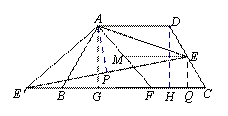
已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
(3)如图3,在(2)的条件下,如果CE=2,AE=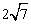 ,求ME的长.
,求ME的长.

解:(1) 30°.
(2)当点E在线段CD上时,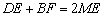 ;
;
当点E在CD的延长线上,
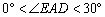 时,
时,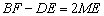 ;
;
 时,
时,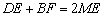 ;
;
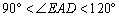 时,
时,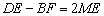 .
.
(3)作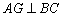 于点G, 作
于点G, 作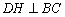 于点H.
于点H.
由AD∥BC,AD=AB=CD,∠BAD=120°,得∠ABC=∠DCB=60°,
易知四边形AGHD是矩形和两个全等的直角三角形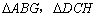 .
.
则GH=AD , BG=CH.
∵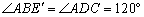 ,
,
∴点 、B、C在一条直线上.
、B、C在一条直线上.
设AD=AB=CD=x,则GH=x,BG=CH=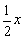 ,.
,.
 作
作 于Q.
于Q.
在Rt△EQC中,CE=2,  ,
,
∴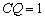 ,
, 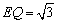 .
.
∴E'Q=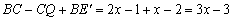 .
.
作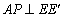 于点P.
于点P.
∵△ADE绕点A顺时针旋转120°后,得到△ABE'.
∴△A EE'是等腰三角形,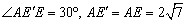 .
.
∴在Rt△AP E'中,E'P= .
.
∴EE'=2 E'P=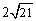 .
.
∴在Rt△EQ E'中,E'Q=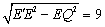 .
.
∴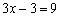 .
.
∴ .
.
∴ ,
,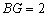 .
.
∴
在Rt△E'AF中,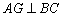 ,
,
∴Rt△AG E'∽Rt△FA E'.
∴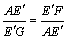
∴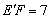 .
.
∴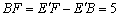 .
.
由(2)知: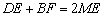 .[来源:Z*xx*k.Com]
.[来源:Z*xx*k.Com]
∴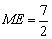 .
.

 高中必刷题系列答案
高中必刷题系列答案 到
到 ,
, ).
).

 D是一个6 × 6网格的示意图,其中每个小正方形的边长为1,位于AD中点处的点P按图2的程序移动.
D是一个6 × 6网格的示意图,其中每个小正方形的边长为1,位于AD中点处的点P按图2的程序移动.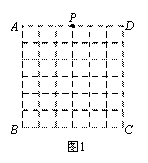

 ,请你化成
,请你化成 的形式,并在直角坐标系中画出
的形式,并在直角坐标系中画出 ,
, 是(1)中图象上的两点,且
是(1)中图象上的两点,且 ,请直接写出
,请直接写出 、
、 的大小关系;
的大小关系; 的根来,要求保留画图痕迹,说明结果.
的根来,要求保留画图痕迹,说明结果.
 中,为必然事件的是
中,为必然事件的是
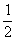 B.
B. C.
C.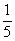 D.
D.
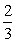 )x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
)x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.