题目内容
已知关于x的方程x2-（a+b）x+ab-1=0，x1，x2是此方程的两个根，现给出三个结论：①x1≠x2；②x1x2＜ab；③x12+x22＜a2b2，则结论正确结论号是 （填上你认为正确结论的所有序号）
考点：根与系数的关系,根的判别式
专题：
分析：（1）可以利用方程的判别式就可以判定是否正确；
（2）根据两根之积就可以判定是否正确；
（3）利用根与系数的关系可以求出x12+x22的值，然后也可以判定是否正确．
（2）根据两根之积就可以判定是否正确；
（3）利用根与系数的关系可以求出x12+x22的值，然后也可以判定是否正确．
解答：解：①∵方程x2-（a+b）x+ab-1=0中，
△=（a+b）2-4（ab-1）=（a-b）2+4＞0，
∴x1≠x2，
故①正确；
②x1x2=ab-1＜ab，故②正确；
③∵x1+x2=a+b，
即（x1+x2）2=（a+b）2，
∴x12+x22=（x1+x2）2-2x1x2=（a+b）2-2ab+2=a2+b2+2＞a2+b2，
即x12+x22＞a2+b2．
故③错误；
综上所述，正确的结论序号是：①②．
故答案是：①②．
△=（a+b）2-4（ab-1）=（a-b）2+4＞0，
∴x1≠x2，
故①正确；
②x1x2=ab-1＜ab，故②正确；
③∵x1+x2=a+b，
即（x1+x2）2=（a+b）2，
∴x12+x22=（x1+x2）2-2x1x2=（a+b）2-2ab+2=a2+b2+2＞a2+b2，
即x12+x22＞a2+b2．
故③错误；
综上所述，正确的结论序号是：①②．
故答案是：①②．
点评：本题考查的是一元二次方程根的情况与判别式△的关系，及一元二次方程根与系数的关系，需同学们熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
计算（-1）2014+（-1）2013的结果是（ ）
| A、1 | B、-1 | C、0 | D、2 |
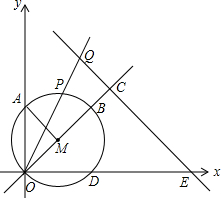在平面直角坐标系xOy中，点M（
