题目内容
【题目】某校初二数学兴趣小组活动时,碰到这样一道题:
“已知正方形![]() ,点
,点![]() 分别在边
分别在边![]() 上,若
上,若![]() ,则
,则![]() ”.
”.
经过思考,大家给出了以下两个方案:
(甲)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ;
;
(乙)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() ;同学们顺利地解决了该题后,大家琢磨着想改变问题的条件,作更多的探索.
;同学们顺利地解决了该题后,大家琢磨着想改变问题的条件,作更多的探索.
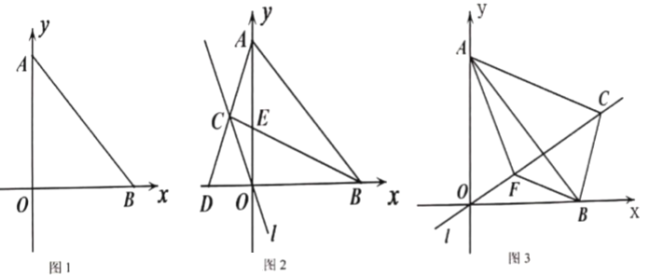
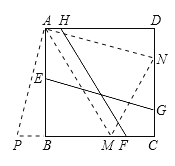
(1)对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图1);


图1 图2
(2)如果把条件中的“![]() ”改为“
”改为“![]() 与
与![]() 的夹角为
的夹角为![]() ”,并假设正方形
”,并假设正方形![]() 的边长为l,
的边长为l,![]() 的长为
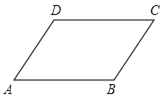
的长为![]() (如图2),试求
(如图2),试求![]() 的长度.
的长度.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)选乙,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,通过证△AMB≌△ADN来得出结论;
,通过证△AMB≌△ADN来得出结论;
(2)按(1)的思路也要通过构建全等三角形来求解,可过点A作AM∥HF交BC于点M,过点A作AN∥EG交CD于点N,将△AND绕点A旋转到△APB,不难得出△APM和△ANM全等,那么可得出PM=MN,而MB的长可在直角三角形ABM中根据AB和AM(即HF的长)求出.如果设DN=x,那么NM=PM=BM+x,MC=BCBM=1BM,因此可在直角三角形MNC中用勾股定理求出DN的长,进而可在直角三角形AND中求出AN即EG的长.
(1)证明:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]()
∴![]() ,
,![]() ,
,
∵正方形![]()
∴![]() ,
,![]() ,
,
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
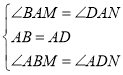
∴![]()
∴![]() 即
即![]() .
.

(2)解:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
将![]() 绕点
绕点![]() 旋转到
旋转到![]() ,
,
∵![]() 与
与![]() 的夹角为
的夹角为![]()
∴![]()
∴![]() ,即
,即![]()
从而![]()
∴![]()
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
解得:![]()
∴![]() .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目