题目内容
 如图所示,O为?ABCD两对角线的交点,E,F分别为OA,OC的中点,图中全等的三角形有
如图所示,O为?ABCD两对角线的交点,E,F分别为OA,OC的中点,图中全等的三角形有
- A.3对
- B.4对
- C.6对
- D.7对
D
分析:本题是开放题,应先根据平行四边形的性质以及三角形全等的判定条件得到△AED≌△CFB,△ODE≌△OBF,△ODA≌△OBC,△ODC≌△OBA,△BCD≌△DAB,△ACD≌△CBA,△DEC≌△BFA.再分别进行证明.
解答:①△AED≌△CFB
∵ABCD是平行四边形
∴AD=BC,∠DAE=∠BCF
∵OA=OC,E,F分别为OA,OC的中点
∴AE=CF
∴△AED≌△CFB;
②△ODE≌△OBF
∵BD为?ABCD对角线
∴OD=OB,∠EOD=∠FOB
∵OE=OF
∴△ODE≌△OBF;
③△ODA≌△OBC
∵BD、AC为?ABCD对角线
∴OD=OB,∠AOD=∠COB,OA=OC
∴△ODA≌△OBC;
④△ODC≌△OBA
∵BD、AC为?ABCD对角线
∴OD=OB,∠DOC=∠BOA,OC=OA
∴△ODC≌△OBA;
⑤△BCD≌△DAB
∵ABCD是平行四边形
∴BC=AD,DC=AB,∠BCD=∠DAB
∴△BCD≌△DAB;
⑥△ACD≌△CBA
∵ABCD是平行四边形
∴∠ADC=∠CBA,AD=BC,AB=CD
∴△ACD≌△CBA;
⑦△DEC≌△BFA
∵DC=AB,DE=BF,CE=AF
∴△DEC≌△BFA.
故选D.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
分析:本题是开放题,应先根据平行四边形的性质以及三角形全等的判定条件得到△AED≌△CFB,△ODE≌△OBF,△ODA≌△OBC,△ODC≌△OBA,△BCD≌△DAB,△ACD≌△CBA,△DEC≌△BFA.再分别进行证明.
解答:①△AED≌△CFB
∵ABCD是平行四边形
∴AD=BC,∠DAE=∠BCF
∵OA=OC,E,F分别为OA,OC的中点
∴AE=CF
∴△AED≌△CFB;
②△ODE≌△OBF
∵BD为?ABCD对角线
∴OD=OB,∠EOD=∠FOB
∵OE=OF
∴△ODE≌△OBF;
③△ODA≌△OBC
∵BD、AC为?ABCD对角线
∴OD=OB,∠AOD=∠COB,OA=OC
∴△ODA≌△OBC;
④△ODC≌△OBA
∵BD、AC为?ABCD对角线
∴OD=OB,∠DOC=∠BOA,OC=OA
∴△ODC≌△OBA;
⑤△BCD≌△DAB
∵ABCD是平行四边形
∴BC=AD,DC=AB,∠BCD=∠DAB
∴△BCD≌△DAB;
⑥△ACD≌△CBA
∵ABCD是平行四边形
∴∠ADC=∠CBA,AD=BC,AB=CD
∴△ACD≌△CBA;
⑦△DEC≌△BFA
∵DC=AB,DE=BF,CE=AF
∴△DEC≌△BFA.
故选D.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 2、如图所示,D为AB边上一点,AD:DB=3:4,DE∥AC交BC于点E,则S△BDE:S△AEC等于( )
2、如图所示,D为AB边上一点,AD:DB=3:4,DE∥AC交BC于点E,则S△BDE:S△AEC等于( )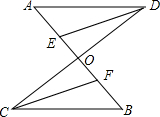 已知如图所示,O为AB、CD的中点,AE=BF,你从图中可以找到全等三角形共( )
已知如图所示,O为AB、CD的中点,AE=BF,你从图中可以找到全等三角形共( )