题目内容
【题目】如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于A(﹣2,0),B两点,与y轴交于C点,tan∠ABC=2. 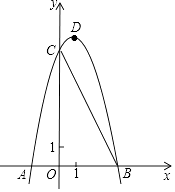
(1)求抛物线的表达式及其顶点D的坐标;
(2)过点A、B作x轴的垂线,交直线CD于点E、F,将抛物线沿其对称轴向上平移m个单位,使抛物线与线段EF(含线段端点)只有1个公共点.求m的取值范围.
【答案】
(1)解:由抛物线的表达式知,点C(0,8),即 OC=8;
Rt△OBC中,OB=OCtan∠ABC=8× ![]() =4,
=4,
则点B(4,0).
将A、B的坐标代入抛物线的表达式中,
得: ![]() ,
,
解得: ![]() ,
,
∴抛物线的表达式为y=﹣x2+2x+8,
∵y=﹣x2+2x+8=﹣(x﹣1)2+9,
∴抛物线的顶点坐标为D(1,9)
(2)解:设直线CD的表达式为y=kx+8,
∵点D(1,9),
∴直线CD表达式为y=x+8.
∵过点A、B作x轴的垂线,交直线CD于点E、F,
可得:E(﹣2,6),F(4,12).
设抛物线向上平移m个单位长度(m>0),
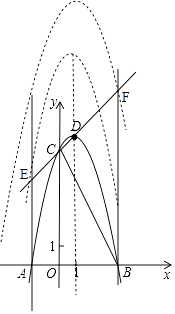
则抛物线的表达式为:y=﹣(x﹣1)2+9+m;
当抛物线过E(﹣2,6)时,m=6,
当抛物线过F(4,12)时,m=12,
∵抛物线与线段EF(含线段端点)只有1个公共点,
∴m的取值范围是6<m≤12
【解析】(1)由OC=8、tan∠ABC=2得点B坐标,将点A、B坐标代入求解可得;(2)先求出直线CD解析式和点E、F坐标,设平移后解析式为y=﹣(x﹣1)2+9+m,结合图象根据抛物线与线段EF(含线段端点)只有1个公共点,求得临界时m的值,从而得出答案,
【考点精析】解答此题的关键在于理解二次函数图象的平移的相关知识,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

 阅读快车系列答案
阅读快车系列答案