题目内容
【题目】如图,以![]() 的直角边
的直角边![]() 为直径的
为直径的![]() 交斜边
交斜边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线与
的切线与![]() 交于点
交于点![]() ,弦
,弦![]() 与
与![]() 垂直,垂足为
垂直,垂足为![]() .
.
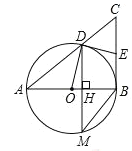
![]() 求证:
求证:![]() 为
为![]() 的中点;
的中点;
(2)若![]() 的面积为
的面积为![]() ,两个三角形
,两个三角形![]() 和
和![]() 的外接圆面积之比为
的外接圆面积之比为![]() ,求
,求![]() 的内切圆面积
的内切圆面积![]() 和四边形
和四边形![]() 的外接圆面积
的外接圆面积![]() 的比.
的比.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)证明∠EDB=∠EBD,则∠BDC=90°,E为直角三角形BDC的中线,即可求解;
(2)△AHD和△BMH的外接圆面积之比为3,确定AD:BM=![]() ,即HM:BH=
,即HM:BH=![]() ,得∠BMH=30°=∠BAC,即可求解.
,得∠BMH=30°=∠BAC,即可求解.
解:![]() 连接
连接![]() ,
,

![]() 是直径,则
是直径,则![]() ,
,
![]() 是切线,
是切线,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() 是圆的切线,
是圆的切线,
![]() ,
,
![]() ,则
,则![]() ,
,
![]() 为
为![]() 的中点;
的中点;
![]() 和
和![]() 的外接圆面积之比为
的外接圆面积之比为![]() ,
,
则两个三角形的外接圆的直径分别为![]() ,
,
![]() ,
,
而![]() ,
,
![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直角三角形的中线,
是直角三角形的中线,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() 的面积:
的面积:![]() ,
,
则![]() ,
,
![]() ,而
,而![]() ,
,
四边形![]() 的外接圆面积
的外接圆面积![]() ,
,
等边三角形![]() 边长为
边长为![]() ,则其内切圆的半径为:
,则其内切圆的半径为:![]() ,面积为
,面积为![]() ,
,
故![]() 的内切圆面积
的内切圆面积![]() 和四边形
和四边形![]() 的外接圆面积
的外接圆面积![]() 的比为:
的比为:![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?